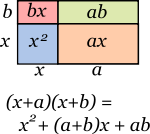Solving Quadratic Equations

Back to Intermediate Algebra

Objective

After working through this section you will: find the values that satisfy a given quadratic equation.

Quadratic Equations

Discussion

What does it mean to solve a quadratic equation?

A quadratic equation is an equation of the form ax²+bx+c=0.

For example, 2x²-7x-15=0.

So, what does it mean to solve a quadratic equation?

Solving a quadratic equation means finding those values of the variable that make the equation true.

For example, solving 6x²+10x+3=7 means finding the values of x that make this equation true.

If x=-2, 6(-2)²+10(-2)+3=7

If x=1/3,6(1/3)²+10(1/3)+3=7

Only these two values of x: -2 and 1/3 make this equation true, so these are the solutions to the equation 6x²+10x+3=7.

How do I find these values of x that make the equation true?

Before we discuss that, there is an important theorem we need to revisit:

Preknowledge

The Zero Factor Principle

If axb=0 then

• a=0
• b=o
• or both a and b are zero.

Now we have reviewed the Zero Factor Principle, we can continue our exploration into solving quadratic equations. We see now that we can solve any factor-equation of the form ab=0.

Activity

Solving a Quadratic Equation

We will look at a specific example of a factorable quadratic equation 6x²+x-15=0 where a = 6, b = 1 and c = -15. Note:the sign on the number must be included.

	ax2+bx+c=0	6x2+x-15=0
Step 1: Multiply a by c.	a x c = ac	6 x -15 = -90
Step 2: Find the factors of ac that add to give b.		-90 = -9 x 10; -9 + 10 = 1
Step 3: Rewrite the equation, represent b as the sum of the two factors you just found.		6x2-9x+10x-15=0
Step 4: Factor the equation by grouping.		3x(2x-3)+5(2x-3)=0
This equation now has two terms that have a common factor of (2x-3), factor again.		(2x-3)(3x+5)=0

Now you have a factor-equation of the form a x b = 0: (2x-3)(3x+5)=0

Here we will use the Zero Factor Principle, so

• 2x-3 = 0, and so solving for x, x = 3/2
• 3x+5 = 0, and so solving for x, x = -5/3

Assignment

Solving Quadratic Equations

Solve the following quadratic equations, using the method shown above:

1. x²-2x-3=0
2. 6x²-x-2=0
3. 2x²-x-6=0

Solutions

1. x²-2x-3=0

                Step 1: 1 x -3 = -3

                Step 2: Factors of -3 that add to -2: 1 and -3

                Step 3: x2+x-3x-3=0

                Step 4: x(x+1)-3(x+1)=0

                           (x+1)(x-3)=0

                        x+1=0 and x-3=0

                     Therefore, x = -1 and 3

Back to Intermediate Algebra