Pedagogical Content Knowledge
Contents
Pedagogical Content Knowledge
| Discussion Many four-digit numbers are used on real life. Search the newspaper and quote ten different examples. e.g.: According to Social Welfare Department's statistics, 4315 children below the age of 19 were involved in prostitution between 1995 and 1999. (source: The Star 27 November 2006 pageN27) Share your findings with your coursemates. |
Numbers to 10 000
Do you know that we use four-digit numbers widely in our daily lives? For example, we have the serial number in certificates, identification number, car number plate, name of a certain year, number of daily calories intake and so on.
The concept of numbers is abstract. Your pupil may be able to write the symbol 2007. This does not mean that the pupil understands the concept of the number two thousand and seven. In order to teach "numbers to 10 000" effectively, you have to understand some basic concepts of numbers.
The written symbol for a number is called numeral. The numeral for the number five thousand three hundred and twenty eight is 5328. In other words, we can say number in words and also write a number in numeral. We use a base of 10 in our number system. Therefore, we only have numerals from 0 to 9.
The starting point for numeration is counting. In Year 2 syllabus, your pupils have learnt numbers to 1000. However, counting does not stop with 1000. The place value positions after hundreds are thousands and ten-thousands.
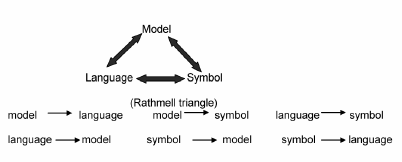
To teach the concept of numbers effectively, we follow the six directions of the Rathmell triangle which relates model (a representation of the objects) with language (name) and symbol in six relationships.
(Source: Tom Cooper, 1999. School of Mathematics, Science and Technology Education, Queensland University of Technology, Australia)
|
The model or a representation of objects for a four-digit number can be shown using the Dienes Blocks or multi-based blocks.

|
The cubes represent thousands. The planes represent hundreds. The rows represent tens. The units represent ones. Using these models, you may introduce the name and the symbol of the numbers. It is important to practice numbers until your pupils become very familiar with them.
Place value chart shows the place value of each digit in a number. A place value chart is shown below.
| thousands | hundreds | tens | ones |
|---|---|---|---|
| 8 | 0 | 4 | 6 |
| 7 | 9 | 0 | 0 |
The digit zero in the two numbers serves as a place holder.
Estimation and Approximation
Discussion:
When you buy a packet of ground nuts, can you estimate the number of ground nuts in the packet? Can you suggest some ways to enhance the skill of estimation?
We teach Year 3 pupils to estimate quantities of objects up to 1000. This can be done by asking the pupils to count in tens, hundreds, and thousands.
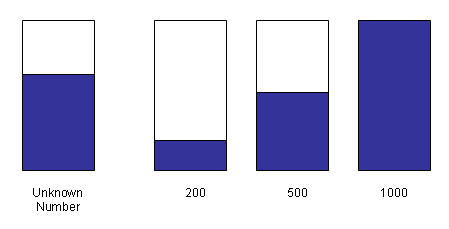
|
We put some red beans in a transparent container. Then, we show three transparent containers with the number of red beans labelled as shown above. Comparing the height of the red beans in similar containers makes it easier for your pupils to estimate the number of red beans of unknown quantity.
When your pupils have acquired the skills of estimation and approximation, they wound be able to check answers in their calculation quickly.
In planning the strategies for teaching and learning activities for the topic of estimation and approximation, you have to ensure that your pupils acquire skills in
(a) Estimation:
- estimate to make wise decision;
- count mentally.
(b) Approximation:
- They understand the concepts of place value of ones, tens and hundreds.
- They know how to round off to an approximate value based on the place value.
Activity 1
| Item | Price (RM) |
|---|---|
| Shampoo | 9.90 |
| Shower Gel | 7.90 |
| Tooth Paste | 8.05 |
| Tooth Brush | 5.15 |
| Soap | 2.40 |
1. Try out the following activity:
(a) Find the total cost of the items in the list.
(b) Find the estimation of the total cost of the items excluding the value of sen.
(c) Find the estimated total cost of the items with rounding off to the nearest ringgit.
2. Compare your answer in each case. What is your conclusion on rounding off?
Addition and Subtraction
Discussion: In the module of teaching Year 2 mathematics, you learnt to teach addition and subtraction of three-digit numbers. What were the emphases in the teaching of these two operations for two-digit and three-digit numbers?
In teaching addition and subtraction of four-digit numbers, you should pay attention to the aspects of
understanding of concepts and the process of regrouping; solving problems involving addition and subtraction in real life situations.
In planning and carrying out teaching and learning strategies, you should be attentive of the following activities.
| Addition is related to counting on. Subtraction is related to counting back. Your pupils acquire the concrete experience informally. You use concrete objects to demonstrate before introducing formal mathematics symbols.
You teach the regrouping process using teaching aids such as Multi-based blocks or abacus. The addition operation is related to the subtraction operation. Subtraction is the inverse of addition. Problem solving questions are based on real life situations. Your pupils have to solve non-routine problems so as to develop their critical and creative thinking skills. |
(Source: Teacher Education Division, Malaysia.1998. Primary School Mathematics Teaching and Learning of Whole Numbers Module.Kuala Lumpur. Page 36.)
Activity 2
Search through the last few years of the Arithmetic Teacher or other journals of teaching Mathematics in Primary Schools. Read an article on the teaching and learning of addition or subtraction of four-digit numbers using non-routine problems.
Discuss your article in the online group forum with your coursemates and tutor.
Relationship of Counting and Operations
To build the concept of four-digit numbers, you may tell your pupils to count on by ones, tens, hundreds, and thousands. Odometer is a name given to the principle which describes the nature of all place-value positions to count like the ones position. For example:
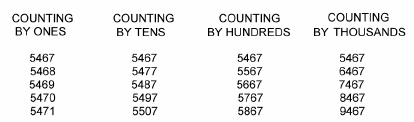
|
(Adapted from: Tom Cooper, School of mathematics, Science and technologyEducation, QUT, 1999)
You have learnt number lines in the earlier modules. Again number lines can be used to show the position of the four-digit numbers.
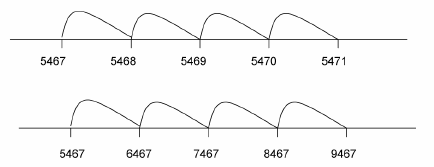
|
The material for teaching counting on is a calculator. For example, enter 5467 and then add 100 and keep pressing =
Similarly, you may tell your pupils to count back. For example:

|
Count on is similar as addition. For example,
| |
On the other hand, count back is like subtraction. For example,
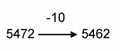
|
Using Abacus
Do you know what an abacus is? It is a calculating tool for performing arithmetic processes such as addtion and subtraction operations. Piaget (1972) said that primary school pupils understand mathematics concept through concrete experience. Thus teaching aids such as Abacus play an important role in showing mathematics concept effectively.
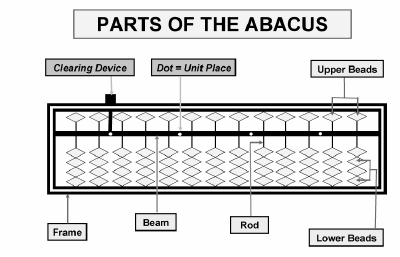
|
How to use Abacus? Before you know how to use Abacus, you need to understand the Abacus structure. The first rod on the right is the place value for ones. The next rods indicate tens, hundreds, and thousands.
Now let us look at the proper technique of using abacus. The thumb and the index finger together with the middle finger are used to manipulate the beads. Beads in lower deck are moved up with the thumb and down with the index finger.
In certain calculations, the middle finger is used to move beads in the upper deck.
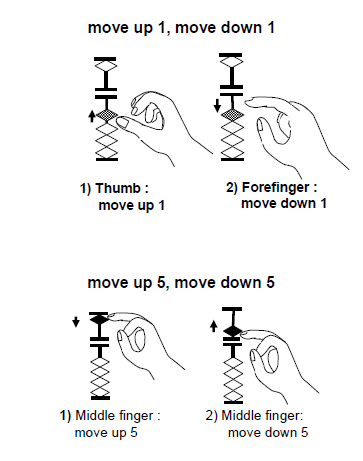
|
Activity 3
Use an abacus to perform addition and subtraction of four-digit numbers. Demonstrate to your pupils the ways to do these operations by using abacus.
What are the benefits of using abacus to perform addtion and subtraction? Discuss in the online group forum with your tutor and coursemates.
Traditional Algorithms
The modern approach in teaching mathematics is that you should allow your pupils to develope their own strategies in written algorithms for performing addition and subtraction operations. The traditional algorithm is not the only way of doing addition and subtraction. However, you need to use concrete materials such as base-10 materials and place value charts to help your student to develop the symbolic algorithms. The process of the traditional addition and subtraction algarithm is shown below. It is based on the sequence of (real world problem) model language symbol.
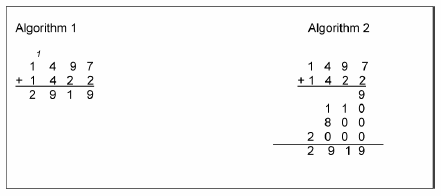
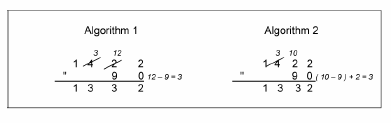
Figure 1 shows two examples of algorithms for addition and Figure 2 illustrates two examples of algorithms for subtraction.
(Source: Adapted from Gan Teck Hock, et al, 2003, KPLI Mathematics Module, Teacher Education Division, Ministry of Education Malaysia, Page 81)
Discussion: Study the algorithms for addition and subtraction carefully. Which of these algorithms do you think is easier for your pupils to follow? Why?
Share your views in the online group forum with your coursemates.