Openphysics/Static electricity

Introduction to electricity - static electricity

We find that electricity in one form or another underlies just about everything in the physical world. It holds atoms together to form molecules, rains down upon the earth as lightning, and sparks between our feet when we scuff a rug. Or comb our hair. The control of electricity is evident in technological devices of any kind; computers, phones, satellites; anything. In this day and age it’s becoming more and more important to have an understanding of how electricity works; in order to acquire this, we need to take a step-by-step approach, as different concepts lead onto the next and so on.

This section looks at electricity at rest, or 'electrostatics', as it is called. This involves electric charges, the forces beween them, the aura that surrounds them and their behviour in materials.

Electrical forces

Electricity is a universal force like gravity, which varies inversely as the square of the distance; except electricity is billions upon billions time stronger than gravity. If gravity was this strong, and an attractive force, then the whole universe would be pulled together into a tiny ball; if it were a repelling force, then the universe would just be an extremely rapidly expanding gaseous cloud. Electricity is neither an attractive nor repelling force; it is both. Positives repel positives, but attract negatives and vice-versa. (Think of magnets attracting and pulling – this will be introduced later on.)
Clusters of positives and negatives have been pulled together by the hugely strong attraction of electrical force. The result is that the huge forces have balanced themselves out almost perfectly by forming compact groups of evenly mixed numbers of positives and negatives. In fact, between two separate bunches of such mixtures, there is practically no electrical attraction or repulsion at all. For example, the electrical forces between the moon and the earth have been balanced out by now. This explains why the much weaker gravitational force, which only attracts is the dominant force.

Electrical charges

The terms positive and negative refer to electrical charge, the fundamental quantity that underlies all electrical phenomena. Protons are positively charged, and electrons negatively charges. The attractive force between protons and electrons is what holds atoms together. Due to the structure of atoms, sometimes electrons can be closer to a neighbouring proton than their own proton – this leads to molecules being formed.

Conservation of charge

In a neutral atom there are as many electrons as there are protons, so there is no net charge. The positive balances the negative perfectly. If an electron is removed or added, the atom gains a positive or negative charge respectively; charged atoms are called ions. All material objects are made out of atoms, so they are composed using electrons and protons (and neutrons). Objects normally have equal numbers of electrons and protons and have no charge, but there can be a slight imbalance when electrons are ripped loose, are added on. The inner electrons are hard to dislodge, however the outer electrons have weaker forces holding them, and can be dislodged much more easily. How easily varies depending on the material in question; rubber and plastic hold onto their atoms with more strength than your hair does for example, so combing your hair with a rubber comb can result in electrons transferring from your hair to the comb. The comb is now negatively charged, and your hair positively.
When an item is charged, no electrons or protons are destroyed; simply transferred; the charge of electricity is conserved much like energy and momentum. In this case, it is simply called the conservation of charge.

Coulomb’s Law

The electrical force, like gravitational force, decreases inversely as the square of thee distances between charges. This relationship was discovered by Charles Coulomb in the eighteenth century and is called Coulomb’s Law. It states that for charged objects that are much smaller than the distance between them, the force between the charges varies directly as the product of the charges and inversely as the square of the separation distance. The force acts along a straight line form one charge to the other. Coulomb’s Law cab be expressed using the formulae:

F = k* (q₁q₂) / d²

Where d is the distance between the charged particles, q₁ represents the quantity of charge of one particle, q₂ represents the quantity of charge of the other particle, and k is the proportionality constant.
The unit of charge, Q, is called the coulomb, abbreviated ‘C’. The charge of 1C is the charge associated with 6.25 billion, billion electrons. This might seem like a great number of electrons, but it only represents the amount of charge that passes through a common 100-watt light bulb in a little over a second. The proportionality constant k in Coulomb’s Law is similar to G in Newton’s law of gravity. Instead of being very small like G (6.67 * 10 ^-11), the electrical proportionality constant k is very large;

K = 9,000,000,000 * (N*m²) / C²

Or, in scientific notation, k = 9*10⁹ N*m²/C². The units N*m²/C² are not central to our interest here, but simply convert the right hand side of the equation to the unit of force, the newton, N. what is important is the large magnitude of k. if, for example, a pair of like charges of 1 coulomb each were 1 metre apart, the force of repulsion between the two charges would be 9 billion newtons; roughly ten times the weight of a battleship! Obviously such amounts of net charge don’t usually exist in our everyday environment.
So Coulomb’s Law for electrical charges is similar to Newton’s law of gravitation for masses, whereas the gravitational force of attraction between particles such as an electron and a proton is extremely small, the electrical force between these particles is relatively huge. The greatest difference between gravity and electricity is that gravity can only be attractive, but electricity can be repulsive or attractive.

Useful videos on Coulomb’s law can be found here:
Introduction: http://www.youtube.com/watch?v=Q0Sz1B3DiSA&NR=1&feature=endscreen

Examples: http://www.youtube.com/watch?v=HrNORhgCrek&feature=relmfu

Khan academy (1: introduction): http://www.khanacademy.org/science/physics/v/electrostatics--part-1---introduction-to-charge-and-coulomb-s-law

Electric fields

Electrical forces, like gravitational forces, act between things that are not in contact with each other, as well as those that are. For both the electrical and gravitational cases, a force field exists that influences charges and masses respectively. The properties of space surrounding any mass can be considered to be so altered that another mass introduced to this region will experience a force. The “alteration in space” caused by a mass is called its gravitational field. We can think of any other mass as interacting with the field and not directly with the mass producing it. For example, when an apple falls from a tree, we say it is interacting with the mass of the earth, but we can also think of the apple as interacting with the gravitational field of the earth. The field plays an intermediate role in the force between bodies. It is common to think of distant rocks and the like as interacting with gravitational fields rather than with the masses of the earth and other bodies responsible for the fields. Just as the space around a planet and every other mass is filled with a gravitational field, the space around every electrical charge is filled with an electrical field – a kind of aura that extends through space.

An electrical field has both magnitude (strength) and direction. The magnitude of the field at any point is simply the force per unit of charge. If a charge q, experiences a force, F, at some point in space, the electrical field at point E at that point is

E = F / q

(Another video) Khan academy (2: electric fields) http://www.khanacademy.org/science/physics/v/electrostatics--part-2

Electrical field lines

Electrical fields can be represented by electrical field lines. (The term, represented is used to imply that the lines don’t actually exist.) An electrical field line is a line drawn in an electric field so that its direction and at any point gives the direction of the electric field at that point.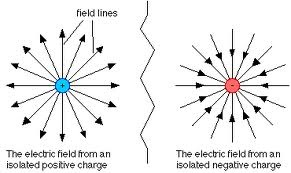

The direction of an electrical field at any point is defined to be the direction of the force on a small positive charge placed at that point. A field line maps out the path of a small positively charged object travelling under the influence of the electrical field. For this reason, field lines are sometimes called lines of force.
Diagrams of electrical field patterns around charged objects shown are drawn by considering the direction in which a small positive charge would move.

The pattern in the last diagram shows a uniform field between the metal plates. The other patterns are radial fields, because the field lines radiate out from, or towards the charges. The patterns outlined above illustrate the following important points:
• Field lines never cross over one another. If they did, it would imply that a force can have two directions at one time – which is impossible.
• The strength of the electric field at any point is shown by the spacing of the field lines. The field is strongest where the field lines are closest together; ie, where the field lines are most dense.
• Field lines start from, or end at charged surfaces at right angles. If they didn’t, there would be some field line along the surface causing the charges to move on the surface. This would change the field line pattern until the field lines were at right angles to the surface. The field lines act as though they are continually trying to shorten their length.

Electric field strength

If q is the charge on a small test sphere which experiences a force, F, in an electric field, the strength of the electric field, E, is given by:

E~ = F~ / q

E~ and F~ are vector quantities, as the direction of E~ is the same as the direction of the force F~ on a small positive charge. (The vector symbol ~ will only be used now in situations where the vector nature is important.)
E~ = F~ / q is often rearranged to give the size of the force on a charge in an electric field:

F = E*q

Example:

Electric potential energy

Gravitational fields and electric fields have some aspects in common. In particular, the concept of gravitational potential energy was developed from the work done in raising a mass against the Earth’s gravitational field. The storage of potential energy in a uniform electric field is developed in a similar way.

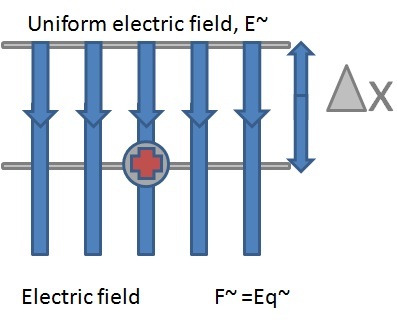
A small test sphere of charge, q, experiences a force, Eq in the direction shown. If the charge, q, is moved a distance ∆x against the field (like lifting mass m against the gravitational field), work is done against the force, Eq, and this work will be stored as potential energy. The work done in moving the charge against the electric field, ∆W, is given by:

∆W = force * distance
=F * ∆x
= Eq * ∆x
∆W = Eq*∆x

The work done is stored in the field and is called electric potential energy.
Electrical energy can be stored in a common device called a capacitor, found in nearly all electronic circuits. Capacitors are used as low-energy on-off switches in computer motherboards, and as a storehouse of larger amounts of energy in photoflash units that release it rapidly during the short duration of the flash.
Example:

Electric potential difference – voltage

The potential energy stored per unit charge is found when the equation ∆W = Eq*∆x is divided through by q:

∆W/q = (Eq*∆x) / q
∆W/q = E*∆x

The potential energy stored per unit charge depends only on the field strength, E, and the distance moved, ∆x. It doesn’t depend upon the charge, and so it is a property of the field itself. The quantity is called the electric potential difference (symbol p.d.) or, voltage (symbol ∆V).

∆V = E∆x

The unit for electric potential difference is the volt (symbol V).
1 volt is 1 joule per coulomb (1V = 1*J *C -1), so when a charge of 1 C moves through a p.d. of 1V, its potential energy changes by 1 J.
In a cell or battery, energy from a chemical reaction is transferred to electrons. EG, a 12V car battery gives 12J of electrical energy to each coulomb of charge it delivers to a circuit.
If electrical contact is made between two differently charged conductors, charge will move from one to the other because there is potential difference between them. (Similar behaviour occurs with differences in pressure and temperature.)

When measuring, it is sometimes appropriate to have a zero reference point. The freezing point of water is the zero reference point for the Celsius scale, and sea level is the zero reference point for the heights of mountains and depths of oceans. For electrical measurements, a convenient zero for electric potential energy is the Earth itself.
A positively charged object has a positive potential and when connected to the earth, electrons move from the earth to the positively charged object until the object is neutral and has zero potential.
A negatively charged object has a negative potential and when connected to the earth, electrons move from the negatively charged object until the object is neutral and has zero potential.
When positive charges are able to move in a conducting liquid or gas, they move from the higher potential to the lower potential.
Ground (or common) is the term usually used in electricity for the point in an electrical circuit having zero potential. If the point is actually connected to the earth via the earth connection on a 3-pin plug, it is called earth.

Potential gradient

The definition of the electric field strength, E = F/q, is difficult to use experimentally because it is hard to measure forces and charges directly. To overcome this, the equation ∆V = E∆x can be rearranged to give
E = ∆V/∆x
The quantities (symbols ∆V and ∆x) can be measured easily using a voltmeter and a ruler, and as a result, the electric field strength E is more easily calculated in a practical situation.
The quantity ∆V/∆x is called the potential gradient. It is a gradient because it is a measure of the change in potential in an electric field as a charge moves through a change in distance ∆x.
The electric field points in the opposite direction in which the potential increases.
If free to move, positive charges move down the potential gradient from a higher potential to a lower one, ie, in the direction of the electric field. (Electric field direction is defined as the direction in which a small positive charge would move.)
If free to move, electrons, being negatively charged, will move up the potential gradient opposite to the electric field direction.
The equation E = ∆V/∆x gives the unit Vm-1 for the electric field strength. This unit is the equivalent of N C^-1.
Example:

Electric shielding

An important difference between electric and gravitational fields is that electrical fields can be shielded by various materials, while gravitational fields cannot (as we know; you can’t just stop gravity from acting on something by placing some metal between two planets!) The amount of shielding is characteristic of the medium within the field. For example, air slightly diminishes the electric field between a pair of charges compared to a vacuum, while oil placed between the charges diminishes the field to about one-eightieth. Metal will completely shield an electric field.
Consider for example, electric charge on a spherical metal shell. Because of mutual repulsion, the charges will spread out uniformly over the outer surface of the shell. It is not difficult to see that the electrical force exerted on a sample test charge placed inside the shell at the exact centre would be zero because opposing forces would balance in every direction. Interestingly enough, complete cancellation will occur anywhere inside the conducting sphere. Understanding why this is true requires more thought and involves the inverse-square law and a bit of geometry.

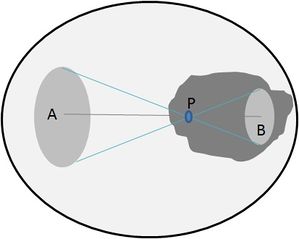
Point P is twice as the distance from the left hand side of the sphere as it is from the right hand side. If electrical force between the test charge (P) and A&B was only decided by distance, then the test charge (P) would be attracted to the left hand side (A) 1/4^th as much (due to the inverse square law: twice the distance means only 1/2² of the effect, and three times the distance means 1/3³ (1/9) of the effect, and so on). However, the force also depends on the amount of charge. Note how the same angle subtends regions A&B, and that no matter what the angle is, A will have four times the area, and therefore 4 times the charge as region B. Since ¼ times 4 = 1, a test charge at P is attracted equally to each side.
If the conductor isn’t spherical, then the charge distribution won’t be uniform. The charge distribution over conductors of various shapes is shown below

Most of the charge on a conducting cube for instance, is mutually repelled to the corners. The neat thing is this: the exact charge distribution over the surface of a conductor is zero. Look at it this way if there were an electric field inside a conductor, then free electrons inside the conductor would be set in motion. How far would they move? Until equilibrium is established – which is to say, when the positions of all the electrons produce a zero field inside the conductor.
Shielding yourself from electric fields is quite simple; just surround yourself or whatever you want to shield with a conducting surface. Put this surface in an electric field of any field strength; the free charges in the conducting surface will arrange themselves on the surface of the conductor in such a way that all field contributions inside cancel each other out. That’s why certain electronic components are encased in metal boxes and why certain cables have a metal covering – to shield them from all outside electrical activity.