Openphysics/Motion
Discuss why a car can go faster around a banked corner compared to a non-banked corner.
Because of the added centripetal force due to the horizontal component of reaction force. The car is able to go faster around a banked corner. Where as when a car goes around a normal corner the reactant force is upward instead of horizontal, the car is not able to go as fast around the non-banked corner.
Contents
Motion
The motion of objects can be described and measured using various quantities such as distance, speed and acceleration.
Motion also involves the direction in which the object is moving. When the direction is important, the scalar quantities of speed and distance must be replaced by the vector quantities of displacement and velocity.
Displacement, velocity and time
Distance and displacement both have the symbol ‘d’, and both measure changes in position; distance however, is a scalar quantity, and only involves the size of the movement – not the direction – whereas displacement involves both the size, and the direction of motion from a reference or starting point.
Similarly, speed only measures the size of motion (change in distance-over-time) whereas velocity measures the size and direction of motion (change in displacement-over-time.)
The formula’s are as follows:
Using vector quantities: d = displacement v = velocity t = time
Using scalar quantities: d = distance v = speed t = time
v = d/t d = v*t t = d/v
Instantaneous and Average speed
Instantaneous speed is the speed something has at any one instance “the dog is running at 2 metres per second”.
Objects don’t always move at steady constant speeds, “Ted’s average speed in the marathon was 6 kilometres per hour”. So the average speed is found by dividing the total distance (or displacement) by the time interval - average speed = total distance/time interval
Most often, it is the average speed that is required for speed/distance/time and velocity/displacement/time problems
Example1:
A car travels 100 metres north in 20 seconds. What is the car’s average velocity?
Displacement = 100 m velocity =? time = 20 s
v = d/t v = 100/20 v = 5
Displacement and time are measured in this case in metres and seconds, so velocity is measured in metres-per-second, or m/s, or ms-1, therefore, the velocity of the car = 5ms-1 north.
Example2:
A boat travels south downriver at a constant speed of 30kmh-1, for 180 minutes. Find how far the boat travelled (its displacement) in kilometres.
Displacement =? velocity = 30kmh-1 time = 180 minutes
The time is given in minutes, but the velocity is kilometres-per-hour, so the time quantity must be converted into hours; 180/60 = 3 hours.
d = v*t d = 30*3 d = 90
Velocity and time are measured in kilometres-per-hour and hours, so displacement is measured in kilometres – as asked - so the boats displacement = 90km south.
Example3:
Example4:
An aeroplane covers a certain distance at a speed of 240 kmph in 5 hours. To cover the same distance in 1 hours, it must travel at a speed of:
solution: Distance = (240 x 5) = 1200 km.
Speed = Distance/Time
Speed = 1200/(5/3) km/hr. [We can write 1 hours as 5/3 hours]
Required speed = 1200 x 3/5 km/hr = 720 km/hr.
A parachutist reaches terminal velocity of 100 kmh-1 and then continues to fall 700 metres before pulling his parachute. How long in seconds is the parachutist falling for?
Velocity is given in kilometres, and displacement in metres; 700 metres = 0.7 kilometres.
t= d/v t=0.7/100 t = 0.007 (hours)
0.007*60 = 0.42 minutes 0.42*60 = 25.2 seconds
The parachutist falls at terminal velocity for 25.2 seconds before activating his parachute
Acceleration
Acceleration is both a scalar and vector quantity. When an object changes in velocity (whether it be slowing down, speeding up or changing direction) the object is said to be accelerating. Acceleration, ‘a,’ is found by the ‘change in velocity’ divided by the ‘time taken for the change in velocity’.
The term acceleration applies to both increases and decreases in velocity (when it is decreasing, then there is deceleration.)
When we travelling in curved path, or one that changes direction, then there is also acceleration –even if we’re moving at a constant speed, because our velocity (directional speed) is changing. It is for this reason that we call acceleration the ‘change-of-velocity-over-time’, as this encompasses changes in speed, and in direction.
If an object travels at a constant velocity – there is no acceleration – the velocity isn’t changing at all. The object has balanced forces acting on it, so with regards to acceleration, it may as well be stationary.
a = v/t v = a*t t = v/a
Acceleration can also be found when the force acting on an object and its mass are known*.
Fnet = m*a a = Fnet/m m = Fnet/a
*information on forces is available below
The units of acceleration vary depending on that of time and velocity:
a = 10kmh/5h a = 2 kilometres per hour per hour, or 2km h or, (most commonly) 2kmh-2
If the units are different, it would look like this:
a = 10kmh / 10s a = 1 kilometre per hour per second, or 1km/h /s, or 1km-1 s-1
Example1:
A bird flying southeast accelerates from 20kmh-1 to 25kmh-1 in 30 minutes. What is the bird’s acceleration?
Change in velocity = 25-20 = 5 time = 30 minutes, = 0.5 hours
a = v/t a = 5/0.5 a = 10 kmh-2
Example2:
A truck is towing a 1,000 kilogram car with a force of 20,000 Newton’s. What is the car’s acceleration?
Fnet = m*a a = Fnet/m a = 20,000 / 1,000 a = 20ms-2
Deceleration problems
Example3:
A ball is kicked east by a football player. The moment the boot makes contact with the ball it travels at 20ms-1, the ball then immediately decelerates, and comes to a halt 10 seconds later.
I) What is the ball’s deceleration?
II) How far does it travel before coming to a stop?
I) vi = 20ms-1, vf = 0 t = 10 s
Change in velocity = 0 - 20 = -20 ms-1
a = v / t a = -20 / 10 a = -2ms-2 deceleration = 2ms-2
Note: the ball immediately decelerates because as soon as it leaves contact with the boot, there are unbalanced forces acting on it. There are no forces pushing it forwards anymore, but there are still forces acting to slow it down, and bring it to a stop (gravity and air resistance while it is in the air, and friction when it rolls on the ground) therefore, the ball immediately decelerates.
II) Average velocity = (20-0) / 2 = 10ms-1
d =v*t d = 10*10 d = 100 metres
The ball’s displacement = 100 metres east.
Further exercises on motion *no answers* are available here http://hrsbstaff.ednet.ns.ca/nmaclell/Science%2010%20and%20O2/pdf%20physics%20science%2010%20part%203.pdf
Circular motion
Circular motion can be used to describe the rotation of an object around an axis; which can be inside, or outside the object. As we have inertia for motion, we have rotational inertia – which affects an objects rotation – and forces applied in certain directions can move objects in circular paths.
A rotation or revolution means motion once around a circle. The time taken to go once around a circle is called the period of rotation (symbol T – measured in seconds). The speed of an object (v) travelling in a circular path can be calculated from the distance travelled and time taken (as with regular motion).
v = d / t
The distance a ball moves around the edge of a circle is equal to its circumference:
d = 2πr
Where r = the circles radius (π is constant).
In general, the speed of a rotating object is found by dividing the distance travelled in one rotation by the time taken for one rotation. If r is the radius (in metres) and T is the period (in S), then the speed v in (ms-1) is:
V = 2πr / T
Example1:
A ball is attached to a rotating barrel with a radius of 2 metres, in 11 seconds it completes one period of rotation. What is the balls speed?
v = d / t
d = 2 πr
r = 2m
t = 11 seconds
v = 4π / 11 = 1.142397329 (10sf)*
v = 1.14 ms-1 (2dp rounding)
The balls speed is 1.14 ms-1
*Note: calculations must be calculated with radians – not degrees (unless the question states degrees).
The frequency of rotation, f, is the number of rotations made per second. The SI unit for frequency is hertz (symbol Hz). Period (T) and frequency (f) are reciprocals of one another:
T = 1 / f or f = 1 / T
In the previous example, the rotation period was 11 seconds – this means the frequency was 1 /11 – so 1 /11 of a rotation was completed each second.
Example1:
A ceiling fan’s blades rotate with a frequency of 20 Hz. The blades have a length of 120 cm; what is the velocity of the spinning blades?
T = 1 / f
T = 1 / 10
T = 0.1
v = 2πr / T
r = 1.20 m
T = 0.1
v = 2.4π / 0.1
v = 24π ms-1*
[or v = 75.3982 ms-1 (4dp rounding)]
The ceiling fan’s blades are rotating at 24π ms-1*
*Note: answers given with π are more accurate than those rounded.
The frequency of rotation is sometimes expressed in a non-SI unit called revolutions per minute (rpm). The frequency in rpm is 60 times greater than the frequency in hertz, because there are 60 seconds in minute.
A car’s rev counter reads an engine speed of 3000 rpm; calculate the frequency in hertz.
Hz = rpm / 60
Hz = 2000 / 60
= 33+1/3 Hz
or 33.33 Hz (4sf rounding)
Rotational inertia
Objects at rest tend to stay at rest, and objects in motion tend to stay in motion without any external forces acting on the object; this also applies to rotation; objects which are rotating continue to rotate unless there is external intervention. An objects ability to resist rotation is its rotational inertia.
Like with inertia for linear motion, an object’s rotational inertia also depends on its mass; but unlike linear inertia, rotational inertia also depends on the distribution of mass in terms of the rotational axis; the greater the distance between the bulk of an object’s mass and its rotational axis – the greater the rotational inertia. Once rotating, objects with high rotational inertia have a higher tendency to remain rotating; if at rest, they have a greater tendency to stay at rest (and not rotate). Tightrope walkers use long poles to stay stable and upright when balancing. This works because the poles have very high rotational inertia; much of the mass is very far from the centre; so when the walker loses balance, he can simply grip the pole – rotating it – and not falling down.
Centres of mass and gravity
When you throw a round ball through the air, it travels in a smooth parabolic curve; but when you throw cricket or baseball bat through the air, its curve will be wobbly. The wobbles aren’t random though; they are rotating around the centre of mass. The ball will also do this; but its centre of mass is located at the centre of the ball, so no changes occur in its path. Baseball bats are not perfectly round, so the object rotates around its centre of mass, which is slightly to the side of the centre of the bat; objects centres of mass do often make relative sense; cones for example, have their centres of mass exactly one-fourth of the way up the cone (although it depends on the thickness of the bat etc).
Often an object’s centre of gravity is referred to – in most cases this is the same thing as a centre of mass – as the centre of gravity is the average position of weight distribution, and as mass and weight are proportional. However, when an object is not under the influence of gravity, the centre of gravity is different (the moon for example has a centre of gravity different to its centre of mass).
Centripetal force
A force that causes an object to follow a circular path is called a centripetal force (centripetal meaning “centre seeking” or “towards the centre”). If centripetal forces cease to act on object, it falls out of its circular path.
If you whirl a lasso or yoyo around in circle, we must keep pulling/swinging on the rope/string to exert centripetal force on the object at the end. The rope/string transmits the centripetal force which pulls the objects into circular paths.
Centripetal forces are not new types of forces; it is simply the name given to the any of the forces (perhaps tension or gravitational – but many other types) which are directed at right angles to the path of a moving object to produce circular motion.
When a car turns a corner, the friction between the tires and the road is the centripetal force that holds the car in its curved path. If the friction isn’t great enough, the car will fall out of its circular path – skidding sideways.
Centripetal force and acceleration
Centripetal forces change object’s directions, but because they are applied at right angles, the speed of the ball never changes. However, the centripetal forces still cause objects to accelerate; they don’t change the object’s velocity; but they do change the object’s direction.
The objects are continually being accelerated inwards towards the centre of the circle. This acceleration is called centripetal acceleration.
If v is the speed of an object rotating around and object in ms-1, and r is the radius of the circle formed in metres, then the centripetal acceleration, a, in ms-2 is:
a = v2 / r
the centripetal force is related to the centripetal acceleration using Newton’s second law:
F = ma
F = m(v2 / r)
F = mv2 / r
Example1:
Often it is easier to calculate the period of rotation, T, rather than the speed of rotation, v. the centripetal acceleration, a, can be calculated for T and r using the formula developed below:
a = v2 / r
a = (2π*r / T)2 / r
a = (4π2*r2 / T2) * (1 / r)
a = (4π2*r) / T2
The centripetal force can be rearranged to:
F = ma
F = (4π2*m*r) / T2
Example1:
Friction prevents a 3kg object from falling off a spinning plate, which rotates at 20 rpm. If the mass is 10 cm from the centre of rotation, what is the friction preventing the mass moving outwards and falling off?
Mass = 3kg
radius = 0.1 m
frequency = 20 rpm
frequency = rpm /60
20/60 = 1/3 Hz
period of rotation = 1/ (1/3)
period of rotation = 3 s
The friction is the centripetal force
centripetal force = F
F = (4π2*m*r) / T2
F = (4π2*3*0.1) / 32
F = 1.2π2 / 9
F = 1.326 N (4sf)
The friction preventing the mass from moving outwards is 1.326 N.
Centrifugal force
When people accelerate, apparent forces are experienced. Eg, when a life accelerates upwards, a person in the lift feels heavier – a greater force then their own weight is acting downwards – which is opposite to the person’s acceleration. A person moving in a circle will experience the same thing; a force pulls them to the outside of the circle (often experienced when a car rounds a corner).
The apparent force experienced towards the outside of a circle is called the centrifugal force and is due to the mass of the object resisting the inward centripetal acceleration that the object is experiencing. A stationary observer outside the circular motion observes the centripetal force only; no centrifugal force is observed; only experienced.
Projectile motion
A projectile is any object that moves through the air without its own source of power; only under the influence of gravity (javelins, bullets, shot puts, baseballs etc).
A very important force that acts on all projectiles is air resistance. Air resistance isn’t constant, but rather changes with the speed of the projectile. Despite being important, it is often ignored in simple problems because it complicates the mathematics in describing object’s motion and solving the problem; so it is assumed the only force acting on an object in flight is its weight force.
This means that projectiles constantly accelerate downwards at the force of gravity (either 10ms-2, or 9.8ms-2 depending on the accuracy required – should be given in question). There is no accelerating force acting horizontally, so the projectiles move horizontally at a constant speed.
Projectile curve
Plotting the path of a projectile gives a smooth parabola.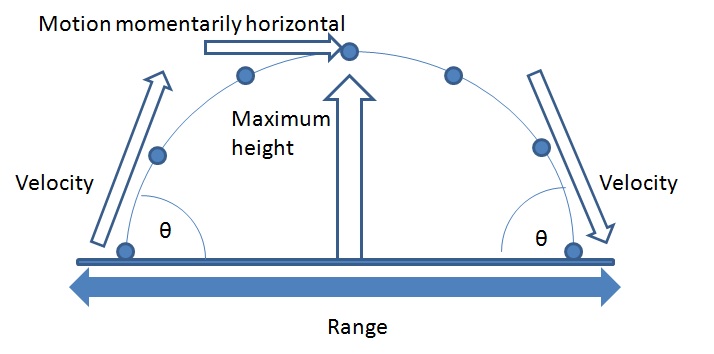
• Projectiles moving horizontally over the ground have their maximum height achieved when the vertical component of the projectile’s velocity is zero (only momentary).
• The total flight time is twice the time is takes to reach the maximum height.
• The distance travelled horizontally (called the range) is the constant horizontal velocity multiplied by the total time of flight.
• The projectile should hit the ground at the same speed that it was fired at and makes the same angle to the horizontal.
Example1:
A discus is thrown with a vertical component of 15 ms-1, and a horizontal component of 20 ms-1. What is the range of the discus?
At maximum height, the vertical component = 0
vf = vi +a*t
0 = 15 + (-9.8*t)
15 = 9.8 * t
t = 1.531 (4sf rounding) seconds
Flight time = twice time taken to reach maximum height.
Total t = 3.062 seconds
Horizontal speed is constant (20ms-1), so we can calculate distance easily.
d = v*t
d = 20 * 3.062
d = 61.24 metres
More exercises are available here: http://www.ece.auckland.ac.nz/oasiss/p/topic/0/ncea2/mechanics2
