Openphysics/MechanicsL2
Contents
Vectors
Vectors and scalars
A vector is a quantity that measures both size and direction; Force is a vector quantity because it is measured in size (how strong the force is) and in what direction it is being applied.
Vectors are drawn as arrowed lines, they have both a tail, and a head (the head points in the direction of the vector, and the tail is the back end.) There are several notations that are used to describe vectors, these include: A~, A~, A, A and A.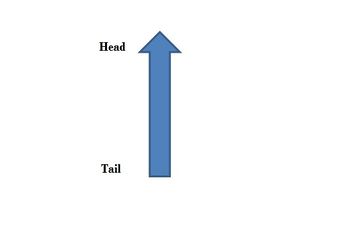
Vectors can be added, subtracted, multiplied and divided by other vectors, as well as multiplied and divided by scalars.
Reference frames
A reference frame is a pair of directions at right angles to each other. These directions are called axes (as in axes on a graph.) Reference frames are used to describe the direction of a vector. The three common reference frames are points on a compass, compass bearings and vertical and horizontal.
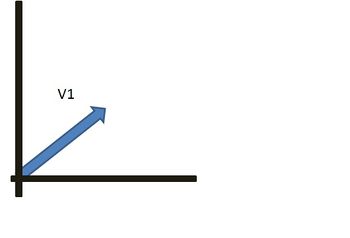
In this reference frame, the vector’s direction (blue line) is given as an angle to north, south, east or west axis; perhaps 30o north of east. It could also be given an angle clockwise from north, EG, 060o (all bearings are given with three digits – beginning with zeros if required). Using a vertical and horizontal reference frame, the east/west axis is horizontal, and north/south vertical; so the vector would be 30o up from horizontal. 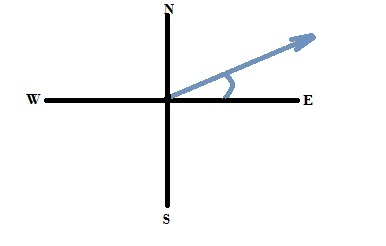
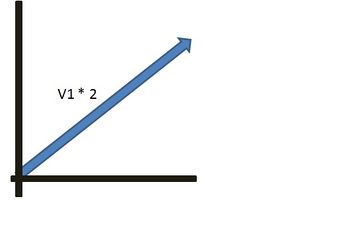
Multiplication of vectors by scalars
Scalars are quantities that only measure size – not direction. Since scalars don’t involve direction, when positive scalars multiply vectors, the direction doesn’t change at all – only the size does.
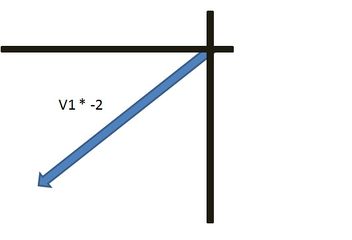
However, if a negative scalar multiplies a vector, the resulting direction is opposite; this should make intuitive sense, as the vector becomes negative, and so its direction turns 180o, and becomes the negative version of the original vector; although different in size as well, as the scalar still multiplies the size.
Addition of vectors
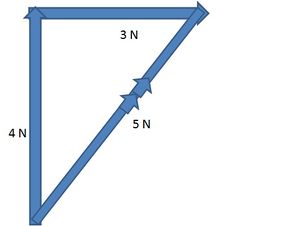
Vectors can be added head-to-tail (in any order) in diagrams so a resultant vector is created. The resultant vector has the same effect as two vectors being added.
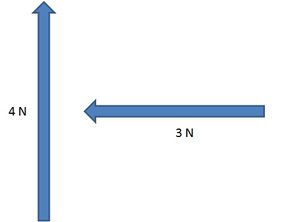
Here we have two force vectors about to be added (4N north, and 3N west)
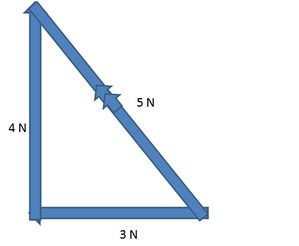
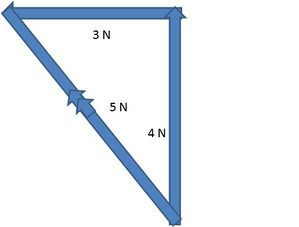
The resultant vector is 5N north-west (not accurate to particular bearings o). The reason it isn’t simply 4N + 3N = 7N, is because the force vectors are acting in different directions, so the net force (represented by the resultant vector) is obviously less than 7N. Instead, Pythagoras theorem for right angled triangles is used. A2 + B2 = C2 in this case, 42 + 32 + = 52 (16 + 9 = 25). The second diagram shows that the vectors may be added in any head-to-tail order, and the resultant vector is still the same.
To avoid confusion – the double arrow midway through the vector shows it is a resultant vector.
Subtraction of vectors
Vectors can also be subtracted in a very similar way, however the order of operations (which vector you subtract from the other) is important. This is to be expected as 3 + 2 = 5 and 2 + 3 = 5, and 3 - 2 = 1, whereas 2 - 3 = -1.
A negative vector is a vector with the same magnitude, but an opposite direction to the original vector.
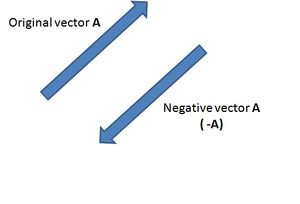
To subtract a vector, you add its negative vector A + (-B) = A - B. By adding the negative vector, you can still use the head-to-tail addition, which is very simple.
We can now subtract the 3N west force vector from the 4N north force vector. To do this, we need the negative version of the 3N west vector - which is a 3N east vector. Next, we add the 4N north vector with the 3N east (-3N west vector), which gives us this resultant vector:
Kinematics
Problems involving uniform acceleration in a straight line over a time interval can often be quickly solved using a set of formulae called the kinematic equations of motion.
vf = vi +at
d = [(vf +vi)/2] * t
d = vi*t + ½ *a*t2
vf2 = vi2 + 2*a*d
d = vf*t – ½*a*t2
if t is in seconds, d is the displacement in metres, vi is the initial velocity in ms-1, vf is the final velocity is ms-1, and a is the acceleration in ms-2.
Forces and torques
Openphysics Forces page: http://wikieducator.org/Openphysics/Forces
Torque
Torque refers the turning effect about a pivot. Torque (or moment, or leverage) is involved in situations such as turning the steering wheel of a car, the turning on/off of a tap or the lifting of a cap of a bottle.
The ’moment of a force’ is the torque that the force produces. The size of a torque depends on the size of the force being applied.
A small force (F) acting at a short distance (d) from a small pivot produces a small torque (t).
The same force acting at a larger distance from the pivot produces a larger torque.
The torque, t, which a force produces about a pivot, is the product of the force, F, and the perpendicular distance, d, of the force’s line of action from the point.
t = Fd
The unit for torque is: newtons*metres, symbol (N m).
Torque can in a sense, be clockwise, or anticlockwise.
Example1:
A tap must be turned with a force of 15 newtons anticlockwise at a distance from the centre of 5 cm. what torque is being applied?
t = Fd
F = 15newtons
Distance = 0.05 metres
0.05*15 = 0.75
Fd = 0.75
t = 0.75 Nm (anticlockwise).
Equilibrium
Torque equilibrium works the same way as all other equilibriums; if the sum of all torques = 0, the object won’t twist or turn – the torque is in a state of equilibrium. This also means that clockwise and anticlockwise moments balance out around any point on the object. (Clockwise moments = anticlockwise moments).
Bridges, planks, trestles and seesaws all involve torque equilibriums (except the seesaw is obviously put out of equilibrium when it is in use).
Example2:
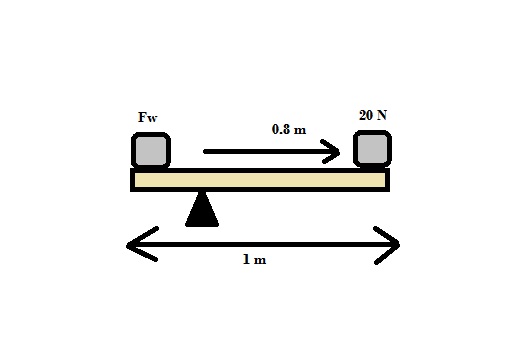
In the diagram above we have a one metre plank of wood (with negligible mass and weight) on a fulcrum 20 cm (0.2m) from the left end. At each end of the plank sits a weight, one of 20 N at the right hand side, and one of unknown weight at the left hand side. Find how much the left weight must weigh in order for the plank to remain in equilibrium.
t = Fd
Right hand weight (clockwise weight) = 20 N, distance from fulcrum = 0.8m
t = 20*0.8 = 16N m (clockwise)
Clockwise moments must equal anticlockwise moments for equilibrium.
t = Fd
Left hand (anti clockwise weight) = Fw N, distance = 0.2N
t = 16 N m for equilibrium
16 N m = 0.2*Fw
16/0.2 = Fw
80 = Fw
Fw = 80 N
Circular Motion and projectile motion
Openphysics Motion page ( which contains projectile and circular motion):
http://wikieducator.org/Openphysics/Motion#Circular_motion
AND: http://wikieducator.org/Openphysics/Motion#Circular_motion
Energy
Energy is one of the most central concepts in all of science; the entire universe is made up of matter and energy. Matter is easily understood; it is what we can touch, taste, see, smell, and hear. Energy on the other hand can be rather difficult, as it is an abstract concept; our sense don’t allow us to examine energy in the same way as matter, and it was even unknown to Isaac Newton, with its existence being debated into the second half of the 19th century. Although it is now more common knowledge, and such a huge part of science, it is hard to define energy, as it is both a thing, and a process – a noun and a verb. Objects (such as people or vehicles and plants etc) have energy, we almost only observe energy when it is transforming (between different forms of energy). Energy can be found in various different forms; it can be transformed from electromagnetic waves being sent off by the sun into heat waves we feel; as well as being harnessed by plants to bind molecules together in photosynthesis; as well as being in the food we eat, which is then harvested when we digest it. It can be found in the tiniest of stationary or moving particles, or possessed by an entire planet.
The best way to start learning about energy is to start by learning about work.]
Work
We’ve learnt about impulse with momentum, where the impulse was the how long a force acted on an object – but ‘how long’ doesn’t need to be measured in time – it can also be measured in distance – and this is where we find work.
W = Fd
Where W = work done (measured in Joules, or Kilojoules) F = force (measured in newtons) and d = the distance (in metres) the object has moved.
When we push a block 10 m across the floor, we are doing work, as a force is being applied to move an object over a distance. However, if we push a much larger block with the same force, but it doesn’t move – no work is done – there is no change in distance (F*0 = 0) so for work to be done, some visible changes must usually take place, or something has to be achieved.
A good example of when work is, and isn’t being done, can be found with weightlifters. Bob, a weightlifter, chooses a 2,000N weight, and hoists it off the ground, to a position above his head – a movement of 2 metres. When he is lifting the weight, he is doing work, and when is fully lifted, he has done 4,000 Joules (2*2000) however, once fully lifted, and he is holding the weight above his head, he is doing no work is done on the weight, as it isn’t moving – there is no change in distance – he may get very tired from holding such a heavy object, but he isn’t ‘achieving’ anything by simply holding it.
- Note: work is a scalar quantity, and the direction of work done doesn’t matter (although vectors can but used for calculations, the resultant vector’s direction isn’t important.)
Example1:
librarian picks up a stack of books with a mass of 3kg, and stacks them on a shelf 170cm higher than their original position. is work being done, and if so, how much?
Work is being done, because the librarian is moving the object’s mass over a distance
the work done is calculated:
W = Fd
W = 30 N * 1.7m (converting Kg into newtons, and cm into m)
W = 51 joules
by lifting and stacking the books, the librarian does 51 joules of work.
Example2:
Power
Power is the rate at which work is done – it essentially measures the rate at which energy is transferred.
Like acceleration measures the change in velocity over time; power measures the change in work done over time:
P = W / t
Where time is measured in seconds, work done in joules, and power in watts (1 watt is 1 joule per second.)
Example1:
A weightlifter lifts a weight of 75 kg off of the ground, and holds it at a position of 200 cm above the ground. The lift takes 3 seconds, calculate the power of the weightlifter.
P = W/t
so first we need to find W (work done)
W = Fd
W = 750 * 2 (converting Kg into newtons, and cm into m)
W = 1,500 joules
P = W/t
P = 1,500 / 3
P = 500 watts
The weightlifter’s power is 500 watts (or joules per second).
Example2:
Potential energy
Objects can store energy because of their position, or their current states; this stored energy is called potential energy (Ep, or PE) because it has potential to do work. Stretched and compressed springs have potential kinetic or elastic energy (this is gone into with more detail in Hooke’s law) as when they are let go of (eg, uncompressed or stretched) they will move and gain kinetic energy. The same applies to bows, slingshots and elastic bands.
Objects such as people, food, or fuels also hold chemical potential energy, as on a microscopic point of view, the atoms are in position to do work; the energy is available to transferred when electrical charges between molecules is altered – when a chemical reaction takes place.
Gravitational potential energy is possessed by objects that are elevated above and against earth’s gravity, as work is required for them to reach this position. Skydivers obviously have a great amount of gravitational potential energy, as when they jump out of aircraft, this potential energy is quickly transferred into kinetic energy. The amount of gravitational potential energy possessed by an object is equal to the work done against gravity for it to reach that position. The work done equals the force required to move it upwards multiplied by the vertical distance it is moved ( W = Fd) the upward force equals the weight (mass multiplied by gravity, or, m*g) so the work done in lifting it through a height is given by the product mass multiplied by gravity multiplied by height; m*g*h.
Kinetic energy
When objects move they posses kinetic energy – due to their motion – and when they slow down or speed up, the kinetic energy is transferred into different forms of energy; when a car slows down by breaking it produces heat and sound, and when it has stopped it has potential energy, and this energy can be converted back to kinetic when it starts moving again.
An object’s kinetic energy is determined by its mass, and the velocity of which it is travelling, shown by the formula:
Ek = ½*m*v2
Where Ek is measured in joules, mass in kilograms, and velocity in metres per second.
More
Example1:
Example2:
Conservation of mechanical energy
In any and every situation where work is done, energy is transferred from one form into another; sometimes several different forms, such as heat, sound and light. What this means is that energy can never be created, and never be destroyed; it is always conserved and transferred. This helps solve many energy related problems, as energy before work is done must equal the total of all forms of energy afterwards (although it can be hard to calculate all the different forms of energy that are produced; for example the energy turned into heat and sound when something loses kinetic energy!)
Hooke’s law
Work is done in compressing or stretching a spring. When this is done, energy is stored in the spring and can be released later. Clocks and catapults use this form of elastic potential energy.
The force needed to extend or stretch an ordinary spring, eg, the spring in a ball point pen, increases as the spring extends. This is also true is the spring is compressed rather than stretched.
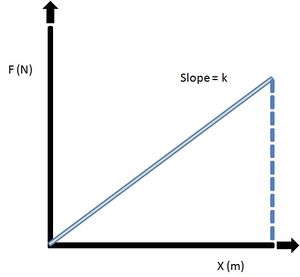
A graph of the extending force against extension shows a linear relationship, if F is the extending force in N, and x is the extension in m, then:
F = k*x
Where k, the slope of the graph – called the spring constant – is measured in N m-1.
The spring’s extension is the extra distance extended. It does not include the spring’s natural length. The elastic potential energy, Ep, stored when the spring is extended (or compressed) a distance x, is equal to the area under the graph from zero to x.
The area under the graph is measured in joules. This comes from multiplying the unit of force (newtons) by the unit of distance extended (metres). The elastic potential energy is shown as the shaded area in the graph below:
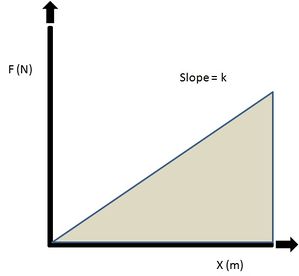
Area = ½ * base * height
Ep = ½ F*x
F = k*x
Ep = ½ (k*x)*x
Ep = ½ kx2
The x2 in the formula Ep = ½ k*x2 shows that proportionally much more (a squared function) elastic potential energy is stored in a spring as it is stretched or compressed further.
Example1:
A mass of 2kg hangs from the end of a spring, extending the spring by 80 cm. Calculate the spring constant, and find how much energy is stored in the spring.
F = m*g
m = 2kg, g = 10
F = 20 N
F = k*x
20 N = k* 0.80
20 / 0.80 = k
k = 25
Ep = ½ k*x2
Ep = ½ 25*0.82
Ep = 8 joules
The spring constant is 25N m-1, and the elastic potential energy is 8 joules.
Momentum
Momentum is all about an object’s mass and velocity; how much ‘oomph’ it has, or how hard it is to stop moving.
We have already covered the ideas of motion and inertia, and momentum is the result of combing the two. For example, we know big trucks with lots of mass are harder to stop in their tracks than smaller cars travelling the same speed, and a giant cruise liner would be even harder to stop; this is because momentum is an object’s mass multiplied by its velocity, given by the formula
p = mv
Where p = momentum, m = mass, and v = velocity (when direction is not needed, v = speed)
Impulses
Changes in momentum occur when there is a change in mass, velocity, or both.
Change in momentum = initial momentum – final momentum ∆p = pi - pf
Most of the time, mass remains unchanged, and velocity increases – this is an increase in momentum, but there is also acceleration – which is produced by forces acting on the object. Clearly then, the larger the force acting on the object, the larger the changes in velocity and momentum will be. However, there is another factor important in changes of momentum: time – how long the force is applied for. For example, if you push a boulder for a split second, its momentum will barely change; but if you push it for a sustained period of time, it will eventually start to roll, or move across the ground. So the largest increases in momentum are found by applying large forces, over long periods of time. The product of force and time is called the impulse.
Impulse = force * time interval Impulse = change in momentum F*∆t = ∆p
If we take a closer look at Newton’s second law, we see the relationship very clearly:
Acceleration is defined as ∆v/∆t and ∆v= vf - vi and ∆p = m*vf -m*vi
F = m*a
F = m*∆v/∆t
F = m*(vf - vi)/ ∆t
Rearranging gives F*∆t = m*vf - m*vi
and at last: F*∆t = ∆p
Consider a car travelling at a high speed. It crashes into a hay stack, and its momentum barely changes. If the same car hit a brick wall of the same mass, it will suffer a huge loss of momentum, and possibly stop moving completely. Why does it appear that the car’s momentum is hurt so much more by the wall than the hay stack? It isn’t because the wall has greater mass – the hay has the same mass – it is because the car makes contact with the hay for a longer period of time, as the hay is loose, whereas the time spent in contact with the wall is much shorter, as the wall is solid, and the change in momentum occurs over a tiny space of time; in fact, the changes in momentum in both cases is the same – it will eventually reach zero; both impulses are the same, but the hay trades less impact force for greater time spent in contact, and the wall has a very small period of impact, so the force of the impact is huge; F = ∆p/∆t.
Example1:
How long must a car tow a 50 KG piece of scrap metal in order for it to increase its velocity from 15 ms-1 to 20 ms-1? The force of the car towing is 100N.
∆p= m*vf –m*vi
∆p= (50*20) – (50*15) = 250 kg ms-1
so the change required in momentum is 250 kg ms-1
now we find the impulse
F*∆t = ∆p
100N*∆t = 250 kg ms-1
∆t = 250 kg ms-1/100N
∆t = 2.5 seconds
The car must tow the piece of metal for two and a half (2.5) seconds.
Conservation of momentum
Momentum is conserved in collisions between objects and in explosions; the total momentum of multiple objects before a collision or explosion equals their total momentum after the collision or explosion. This relationship relies on one key factor; that there are no external forces present; such as gravity or friction. Momentum will be conserved if these forces don’t apply, or if they’ve been balanced by reactant forces.
Momentum is conserved in all directions, meaning vector momentum diagrams are often used to solve problems involving momentum in two dimensions.
Problems involving collisions or explosions must be solved by using conservation of momentum, as kinetic energy isn’t conserved in these scenarios, and can’t be used to solve them.
Conservation of momentum in a straight line (one dimension)
One dimensional conservation of momentum is the simplest conservation situation. problems of this kind can be solved using the formula:
m1u1 + m2u2 = m1v1 + m2v2
m1 and m2 are the masses of the 2 objects, u1 and u2 are the velocities of the 2 objects prior to collision, and v1 and v2 are the velocities of the 2 objects after collision.
Example1:
Two cars crash in a head-on collision. The first car has a mass 1,000 kg, and is travelling at 25 ms-1. The second car has a mass of 1,500 kg, and is travelling at 20ms-1. Find the initial momentum of each car before the crash, and then find the velocity (so include direction relative to the cars) of the wreck formed by both cars after the crash.
Find momentum
Car1
p = mv
p = 1,000 * 25
p = 25,000
p = 25,000 kg ms-1
Car2
p = mv
p = mv
p = 1,500 * 20
p = 30,000 kg ms-1
Momentums prior to crash:
car1 = 25,000 kg ms-1
car2 = 30,000 kg ms-1
find combined velocity after crash
m1u1 + m2u2 = m1v1 + m2v2
1,000*25 + (-1,500*20) = 1,000*v1 + 1,500*v2 (the cars are moving in opposite directions, which is why the minus sign is present; the final wreck is combined, and moving in the same direction, so the momentums are still added on the right-hand side).
25,000 - 30,000 = 1000*v1 + 1500*v2
the momentum is 5,000 kg ms-1 – not negative 5,000 – this has again occurred because of opposite directions, and the amount is changed to ve+ 5,000.
5,000 = 1000*v + 1500*v
the velocity of the wreck is combined, therefore v1 = v2, and we can simply use v
5,000 = v (1000 + 1500) Factorising, as both terms on the right-hand side feature v
5,000 / 2,500 = v dividing both side by (1000 + 1500) or 2500 to solve for v
5,000 / 2,500 = 2
v = 2 ms-1
the direction of the velocity is determined by which car has the highest momentum going into the crash – in this case, car2 – so the velocity of the wreck is 2ms-1 in the direction car2 was travelling.
this is the velocity directly after the collision - friction will begin to decelerate the wreck, as the driver's of the car's should've been braking (or at least not accelerating) resulting in unbalanced forces where friction is greater than the forward forces being produced, and so deceleration occurs.
Conservation of momentum in multiple directions (two dimensions)
Two dimensional conservation of momentum is the more complex than one dimensional conservation of momentum, as one object may move at different angles to other objects, so the angle must be taken into account. A momentum vector diagram can be drawn for problems involving momentum in two dimensions.
Some more exercises are available here: http://www.ece.auckland.ac.nz/oasiss/p/topic/0/ncea2/mechanics2