Name

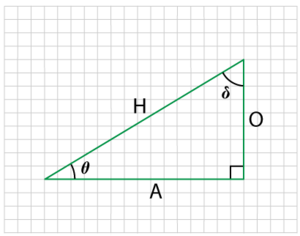
**Trigonometric ratios of Complementary Angles**
Figure	Let
	[math]\triangle AOH:\,[/math] [math]O=\text{ side adjacent to angle }\theta\,[/math] [math]A=\text{ side opposite to angle }\theta\,[/math] [math]H=\text{ hypotenuse}\,[/math] [math]\delta=90-\theta\,[/math]


Trigonometrical ratio of angle [math]\theta\;[/math]	Trigonometrical ratio of complementary angle [math]\delta=90-\theta\;[/math]	Formulas
[math]\sin \theta=\frac{O}{H}[/math]	[math]\cos \delta=\frac{O}{H}[/math]	[math]\sin \theta=\cos \delta\,[/math]	[math]\sin \theta=\cos (90-\theta)\,[/math]
[math]\cos \theta=\frac{A}{H}[/math]	[math]\sin \delta=\frac{A}{H}[/math]	[math]\cos \theta=\sin \delta\,[/math]	[math]\cos \theta=\sin (90-\theta)\,[/math]
[math]\tan \theta=\frac{O}{A}[/math]	[math]\cot \delta=\frac{O}{A}[/math]	[math]\tan \theta=\cot \delta\,[/math]	[math]\tan \theta=\cot (90-\theta)\,[/math]
[math]\cot \theta=\frac{A}{O}[/math]	[math]\tan \delta=\frac{A}{O}[/math]	[math]\cot \theta=\tan \delta\,[/math]	[math]\cot \theta=\tan (90-\theta)\,[/math]
[math]\sec \theta=\frac{H}{A}[/math]	[math]\csc \delta=\frac{H}{A}[/math]	[math]\sec \theta=\csc \delta\,[/math]	[math]\sec \theta=\csc (90-\theta)\,[/math]
[math]\csc \theta=\frac{H}{O}[/math]	[math]\sec \delta=\frac{H}{O}[/math]	[math]\csc \theta=\sec \delta\,[/math]	[math]\csc \theta=\sec (90-\theta)\,[/math]

Usage