LowVision
*To discover why we need to study Mathematics
|
Contents
Why Do We Study Mathematics?
Mathematics and Statistics is one of the eight Learning Areas described in The New Zealand Curriculum. This curriculum is designed to address the needs of today's young people in NZ, so that they can reach their potential in their future lives. Estimating how long it will take you to get to work, following steps in a recipe, calculating your change in a shop and managing your finances all require an understanding of Mathematical concepts.Mathematics is the exploration and use of patterns and relationships in quantities, space and time. Statistics is the exploration and use of patterns and relationships in data. These two disciplines are related but require different ways of thinking and of solving problems [1]. The skills and concepts needed to explore these two disciplines are developed throughout a students education.
The process begins before a child begins school, many children develop a basic understanding about numbers and will be working towards understanding concepts such as: classification (discriminating, matching and categorizing); Seriation (ordering objects, quantities and numbers according to specific criteria); Conservation (that a given amount remains the same though its appearance may change); and Position in Space (such as top, bottom, around and beside). Once a child has developed an understanding of these concepts they will be able to successfully work with formal Mathematical concepts that are developed in school.
Teaching Mathematics to young people who are blind or who have Low Vision is essential for exactly the same reasons that it is essential for their sighted peers. A thorough grounding in mathematics enhances educational and occupational opportunities for all people, whether sighted or visually impaired. In day-to-day routines, a practical understanding of Mathematics allows a person to function more successfully and independently (Kapperman, Heinze & Sticken, 2000). The challenge for the Blind and Low Vision students is that many aspects and concepts used in Mathematics are extremely visual and spatial in nature. This presents a real challenge for educators to provide appropriate teaching resources and strategies that enable these learner's to fully grasp these concepts.
Grasping a Concept
Finally discuss the activity together. Consider which aspects of completing the task were most difficult. What would have made the task easier?
|
Why does a Visual Impairment Make Mathematics Difficult?
Children with little or no usable vision experience the world through their ears, their fingers, their skin, their noses, their mouths, and their movements. Because of this difference in learning, children who are blind or visually impaired will not generally develop on their own the same kinds of concepts about the world as their peers with sight do (Braille Mathematics Standards, 2006). It is more difficult for a blind child to generalize concepts, such as 'big', to include the concept of 'tall'. A 'big sister' would be observed to be taller by a sighted child but this may need to be demonstrated to a child with no vision. With a reduced visual acuity the opportunities for incidental learning are diminished, which necessitates the need to create time for deliberate learning opportunities. Along with time for instruction. Tactile skills are not nature to all children who are Blind of who have Low Vision, for some they need instruction and demonstration. Such children will benefit from development of a systematic approach to tactile exploration. Acquiring information about an objects: texture, hardness, temperature, shape/size/volume, weight and global shape all require different types of touch.
Along with good tactile exploration skills it is essential to establish a good Mathematical vocabulary. Some children are exposed to a rich visual language by the people around them that can see. However, much of this language will lack meaning for them. This can lead to a use of language which masks a deficit in real conceptual understanding. Assessment of understanding should be an ongoing process. In order to ensure that meaning develops with the language it is necessary for a child to be exposed to a rich sensory environment. For many blind and low vision learners a lack of appropriate learning material can inhibit concept development and Mathematical understanding. Modification and adaption of materials and teaching strategies is essential.
The need for modification and adaptation in materials can become an increasing problem as a child progresses through school. For students with low vision who have managed early print, which is generally large and bold, difficulties arise as text gets smaller and pages become more cluttered. Maths notation is typically very small, text books use complicated and cluttered formatting with images embedded in the text that are small and detailed.
How Can Mathematics be Made Accessible to Blind and Low Vision Learners
Pre School
Some general ideas are listed below:
| Strategy/Modification | Description |
|---|---|
| Time to Explore | exploration takes longer without the use of vision |
| Direct Instruction | some clear learning goals for concepts that need development need to be identified and then explored with support |
| Appropriate Materials | need to be constantly available, lots of real objects (shells, buttons, cups, pans, spoons, seaweed, leaves, buckets etc) |
| Lots of Hands On Experience | cooking, building, washing. |
| An Organized and Predictable Environment | creating clearly defined spaces for activities is important to avoid frustrations e.g. a tray and pot arrangement for counting beads to stop them rolling away |
At School
Some general ideas are listed below:
| Strategy/Modification | Description |
|---|---|
| Time | for exploration |
| Time | for direct instruction in Braille Maths, tactile skills, methodology and use of alternative materials/equipment |
| Use of Real Objects | especially in the early years at school. It is important that the objects have meaning for the child. An elephant is real, but a spoon is something most children will have a real experience of using |
| Opportunities to Manipulate | constructing and taking things apart |
| Relate things Back to The Body | difficult concepts such as 'angles' should initially be explored in relation to your body e.g. the angle between your arms held out from the body |
| Encourage Good Tactile Discrimination | some children will need to be encouraged especially when they are 'tactile defensive' |
| Encourage Good Memory Skills | for listening to instructions and information |
| Braille Maths | both reading and writing skills for those students that use it. It will be necessary for the Maths teacher to teach symbols before they are introduced in class. |
| Use of Consistent and Unambiguous Language | each maths symbol must have ONE specific name to avoid confusion. See materials such as 'The Handbook of Spoken Mathematics.' Promote the use of rich descriptive language - Avoidance of 'here', 'there' etc. |
| Encourage Systematic Approaches to Exploration | E.g. use of systems like the WESSTTT (Weight, Edges, Size, Shape, Texture, Temperature, Time) |
| Appropriate Materials/Equipment Available | tactile diagrams, Braille text books, abacus, talking calculators, audio graphing calculators, wikki sticks, tactile protractors, tactile rulers, tactile tape measures, tray and containers, Braille machine, drawing boards, tactile clocks and watches, talking stopwatches, talking scales, solid angle blocks, 2-D shapes, 3-D shapes etc. |
Specific Strategies and Adaptations
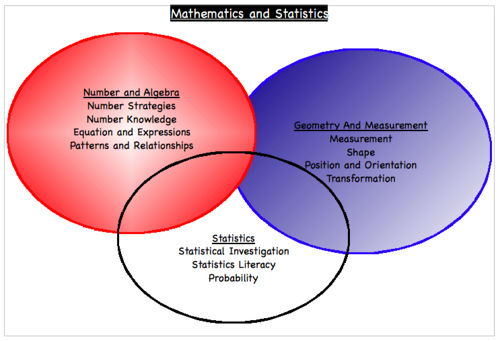
Between Levels 1 and 6 there are three strands to the Mathematics Curriculum in NZ. These are shown in the diagram, which demonstrates the interconnected nature of the three strands.Each strand will require different adaptations and modifications. Some equipment may be possible to use in all areas whilst other bits will only be used in one. For a detailed look at the Strand - Geometry and Measurement please follow the link below.
References
- Californian Department of Education (2006). Braille Mathematics Standards. Sacramento, California: Californian Department of Education.
- Kapperman, G., Heinze, T. & Sticken, J. (2000). Mathematics. In A.J. Koenig & M.C. Holbrook (Eds.). Foundations for education for blind and visually handicapped children and youth: Theory and practice. (2nd ed.). Austin: Texas School for the Blind and Visually Impaired.