Lines with different slopes
The most intuitive way to describe a line is by its slope which tells us how steep the line is, whether it is slanted to the right or to the left, or whether the line is a horizontal or a vertical line. A line with a positive slope slants to the right, and the larger the slope, the steeper the line. A line with a negative slope slants to the left and, the larger the slope, the greater the steepness of the line. A horizontal line has no slant and therefore, has a slope of 0. The slope of a vertical line is undefined. (The reason why will be obvious in the next section.)
Lines with positive slopes
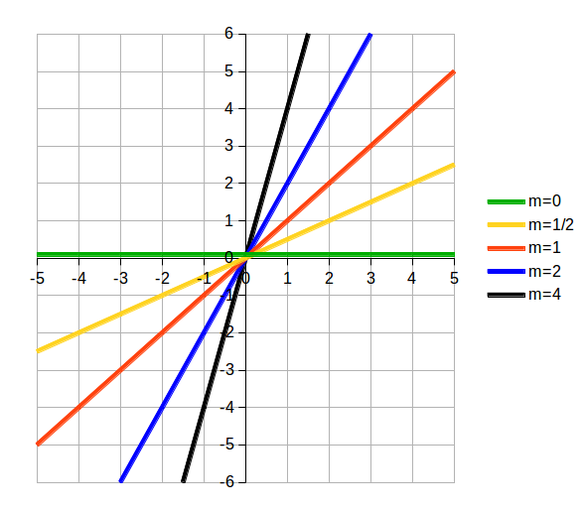
In Graph A at right:
- Note that in the legend on the right, the variable m is used to indicate a line's slope.
- The green line has a slope of 0; it is horizontal and has no steepness.
- The yellow line, which has a little steepness, has a slope of 1/2.
- The red line, which has some steepness, has a slope of 1.
- The blue line, which is steeper than the line with a slope of 1, has a slope of 2.
- The black line, the steepest of all, has a slope of 4.
A line with a slope of 10 would be steeper than all of the other lines shown, and a line with a slope of 1/4 would have a slant somewhere between the yellow line with slope of 1/2 and the green line with slope of 0.
Lines with negative slopes
The other lines now have negative slopes and slant downwards from left to right. Each slope is the negative for the same-color line in Graph A.
The values for the slope (m) of each line are shown in the legend on the right.
Vertical lines
The slope of a vertical line, as shown in the graph at left, is undefined.
