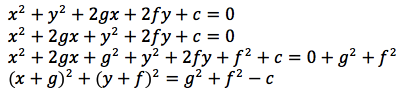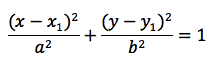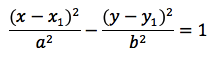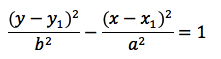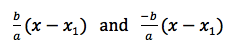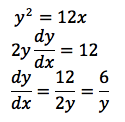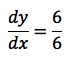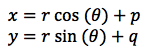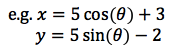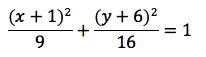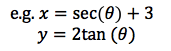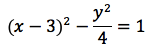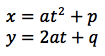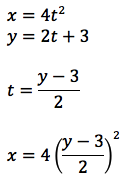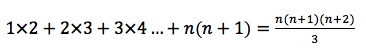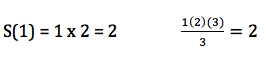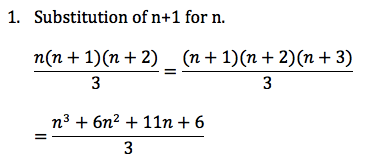Level 3 Calculus - Conics
Contents
The Circle
Delta textbook chapter 37, pages 356 – 360, exercises 37.1 – 37.2
Symbols:
r = radius
s = distance
g and f = a and b.
The standard equation for a circle is:
The general equation of a circle is:
we show that this is true by the process of completing the square (follow the algebra):
--
If you are given a co-ordinate you can find the distance it is from the centre of a circle at (0,0) by the equation:
Similarly, if you a given a co-ordinate you can find the distance it is from the centre of a circle that has been moved from (0,0), or the distance from another point, by the equation:
There is a three-way simultaneous equation example found in the textbook that I was not sure I was allowed to upload - I don't think it's a very common question but go check it out.
The Ellipse
Delta textbook chapter 37, pages 360 – 363, exercise 37.3
The standard equation of an ellipse is:
where a and b are bigger than 0 and x1 and y1 move the ellipse.
a gives the intercepts on the x-axis (centre 0,0), while b gives the intercepts on the y-axis (centre 0,0).
An ellipse has two foci (singular: focus) which lie on the same y-value as a, but sit at –c and c for their x-values.
The relationship to find c is given by:
Don’t forget to translate the foci if the centre has been moved!
The longer axis is called the major axis, and this is usually 2a.
The shorter axis is called the minor axis, and this is usually 2b.
However, the ellipse can be a vertical oval instead of a horizontal one and be stretched a different way. This happens when b is bigger than a.
Completing the square for an ellipse: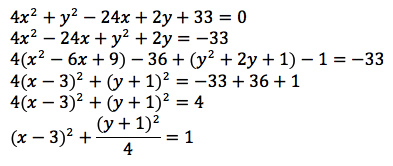
From the two foci, F2 (right focus) F1 (left focus) and the point P on the ellipse, the sum of the distances PF1 + PF2 is constant.
The Hyperbola
Delta textbook chapter 37, pages 364 – 368, exercise 37.4
The standard equation of a hyperbola is:
If the hyperbola is vertical rather than horizontal, the equation changes to be:
...where a and b are larger than 0.
a gives the x-intercepts on a horizontal hyperbola (centre 0,0) while b gives the y-intercepts on a vertical hyperbola (centre 0,0).
The equations for the asymptotes of a hyperbola are:
A hyperbola also has two foci, and they are found through the relationship:
Don’t forget to translate the foci and the asymptotes if the centre has been moved!
Completing the square for a hyperbola: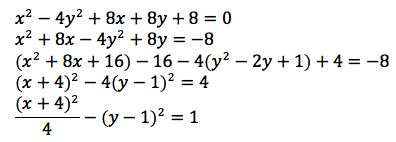
The Parabola
Delta textbook chapter 37, pages 368 – 372, exercise 37.5
The standard equation for a horizontal parabola is:
The focus of a parabola is at (a, 0) for a parabola with centre (0,0).
The directrix, a line behind the parabola, is at x = -a
A parabola with its centre moved has the equation:
The latus rectum is a line which is vertical from the point a (the focus) and extends upwards by a length of 2a and downwards by a length of 2a.
A vertical parabola has the standard equation form:
Don’t forget to translate the focus when a parabola’s centre has been moved!
Applications
Delta textbook chapter 37, pages 372 – 375, exercises 37.6 and extension exercise 37.
Tangents and Intersections
Delta textbook chapter 38, pages 376 – 377, exercise 38.1
A straight line and a conic function can have three different relationships:
1 - Intersection at two points
2 - Tangent
3 - No intersections
Use the method of solving simultaneous equations to solve where the line equation and the curve equation intersect.
The result is always a quadratic that you can solve to find out which relationship the line has to the conic function.
Equations of Tangents and Normals to Conic Sections
Delta textbook chapter 38, pages 378 – 379, exercise 38.2
To find the gradient of a conic section at a certain point we have to differentiate implicitly (get y on one side, x on the other and then differentiate) and then substitute in the given point values.
e.g.
So at (3, 6)
The gradient equals 1.
To find the equation of a tangent:
Substitute this gradient (m) and given point values (x1 (3) and y1 (6)) into the equation: (y - y1) = m(x - x1)
Rearrange the equation so that it equals 0.
To find the equation of the normal:
Divide the gradient by -1. This is your normal gradient.
Substitute the gradient (m) and given point values (x1 (3) and y1 (6)) into the equation: (y - y1) = m(x - x1)
Rearrange the equation so that it equals 0.
Conic Sections in Parametric Forms
Delta textbook chapter 38, pages 379 – 383, exercises 38.3, 38.4, 38.5 and 38.6
The parametric equations of a circle are:
Where r is the radius and p and q are how far the centre of the circle has moved.
To change these equations into the standard equation for a circle change cos and sin to x and y, plus or minus the opposite of p or q off them respectively, and make that equal the r value squared.
turns into:
The parametric equations of an ellipse are:
Where p and q are how far the centre of the ellipse has moved.
To change these equations into the standard equation for an ellipse change cos and sin to x and y, plus or minus the opposite of p or q off them respectively as well as dividing by a^2 and b^2 respectively.
turns into:
The parametric equations of a hyperbola are:
Where p and q are how far the centre of the hyperbola has moved.
To change these equations into the standard equation for a hyperbola, follow the exact same process of an ellipse, but with sec and tan as x and y.
turns into:
The parametric equations of a parabola are:
where p and q are how far the centre of the parabola has moved.
To change these equations into the standard equation of a parabola we have to eliminate t.
e.g.
Induction
Delta textbook chapter 39, pages 387 – 389, exercise 39.1
Given the equation:
Prove this result by induction.
First step: Show that it is true for n=1.
So n=1 is true.
Second: State that you assume the result is also true for S(n).
Third: Show that it is true for n+1.
You prove this by showing that the substitution equals the same thing as when you add the new term to both sides.
2. Adding (n+1) to each side. This is done by substituting n+1 in for n of the last term and adding it on the end.
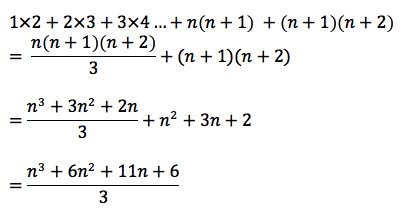
Which is the same result we got when substituting straight in to the equation.
So the result is true for n+1 therefore we have proved it by induction.
Divisibility Proofs
Not covered in the standard as far as I know. Check out the Delta textbook if you think it's important.