K-Nearest Neighbors

In pattern recognition, the k-nearest neighbors algorithm (k-NN) is a method for classifying objects based on closest training examples in the feature space. k-NN is a type of instance-based learning, or lazy learning where the function is only approximated locally and all computation is deferred until classification. The k-nearest neighbor algorithm is amongst the simplest of all machine learning algorithms: an object is classified by a majority vote of its neighbors, with the object being assigned to the class most common amongst its k nearest neighbors (k is a positive integer, typically small). If k = 1, then the object is simply assigned to the class of its nearest neighbor.

The same method can be used for regression, by simply assigning the property value for the object to be the average of the values of its k nearest neighbors. It can be useful to weight the contributions of the neighbors, so that the nearer neighbors contribute more to the average than the more distant ones. (A common weighting scheme is to give each neighbor a weight of 1/d, where d is the distance to the neighbor. This scheme is a generalization of linear interpolation.)

The neighbors are taken from a set of objects for which the correct classification (or, in the case of regression, the value of the property) is known. This can be thought of as the training set for the algorithm, though no explicit training step is required. The k-nearest neighbor algorithm is sensitive to the local structure of the data.Template:Citation needed

Nearest neighbor rules in effect compute the decision boundary in an implicit manner. It is also possible to compute the decision boundary itself explicitly, and to do so in an efficient manner so that the computational complexity is a function of the boundary complexity.

Algorithm

Example of k-NN classification. The test sample (green circle) should be classified either to the first class of blue squares or to the second class of red triangles. If k = 3 it is classified to the second class because there are 2 triangles and only 1 square inside the inner circle. If k = 5 it is classified to first class (3 squares vs. 2 triangles inside the outer circle).

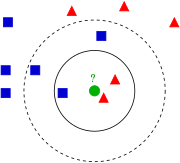
The training examples are vectors in a multidimensional feature space, each with a class label. The training phase of the algorithm consists only of storing the feature vectors and class labels of the training samples.

In the classification phase, k is a user-defined constant, and an unlabelled vector (a query or test point) is classified by assigning the label which is most frequent among the k training samples nearest to that query point.

Usually Euclidean distance is used as the distance metric; however this is only applicable to continuous variables. In cases such as text classification, another metric such as the overlap metric (or Hamming distance) can be used. Often, the classification accuracy of "k"-NN can be improved significantly if the distance metric is learned with specialized algorithms such as e.g. Large Margin Nearest Neighbor or Neighbourhood components analysis.

A drawback to the basic "majority voting" classification is that the classes with the more frequent examples tend to dominate the prediction of the new vector, as they tend to come up in the k nearest neighbors when the neighbors are computed due to their large number.Template:Citation needed One way to overcome this problem is to weight the classification taking into account the distance from the test point to each of its k nearest neighbors.

KNN is a special case of a variable-bandwidth, kernel density "balloon" estimator with a uniform kernel.

Parameter selection

The best choice of k depends upon the data; generally, larger values of k reduce the effect of noise on the classification, but make boundaries between classes less distinct. A good k can be selected by various heuristic techniques, for example, cross-validation. The special case where the class is predicted to be the class of the closest training sample (i.e. when k = 1) is called the nearest neighbor algorithm.

The accuracy of the k-NN algorithm can be severely degraded by the presence of noisy or irrelevant features, or if the feature scales are not consistent with their importance. Much research effort has been put into selecting or scaling features to improve classification. A particularly popular approach is the use of evolutionary algorithms to optimize feature scaling. Another popular approach is to scale features by the mutual information of the training data with the training classesTemplate:Citation needed.

In binary (two class) classification problems, it is helpful to choose k to be an odd number as this avoids tied votes. One popular way of choosing the empirically optimal k in this setting is via bootstrap method.

Properties

The naive version of the algorithm is easy to implement by computing the distances from the test sample to all stored vectors, but it is computationally intensive, especially when the size of the training set grows. Many nearest neighbor search algorithms have been proposed over the years; these generally seek to reduce the number of distance evaluations actually performed. Using an appropriate nearest neighbor search algorithm makes k-NN computationally tractable even for large data sets.

The nearest neighbor algorithm has some strong consistency results. As the amount of data approaches infinity, the algorithm is guaranteed to yield an error rate no worse than twice the Bayes error rate (the minimum achievable error rate given the distribution of the data). k-nearest neighbor is guaranteed to approach the Bayes error rate, for some value of k (where k increases as a function of the number of data points). Various improvements to k-nearest neighbor methods are possible by using proximity graphs.

For estimating continuous variables

The k-NN algorithm can also be adapted for use in estimating continuous variables. One such implementation uses an inverse distance weighted average of the k-nearest multivariate neighbors. This algorithm functions as follows:

1. Compute Euclidean or Mahalanobis distance from target plot to those that were sampled.
2. Order samples taking for account calculated distances.
3. Choose heuristically optimal k nearest neighbor based on RMSE done by cross validation technique.
4. Calculate an inverse distance weighted average with the k-nearest multivariate neighbors.

The optimal k for most datasets is 10 or more.Template:Citation needed That produces much better results than 1-NN. Using a weighted k-NN, where the weights by which each of the k nearest points' class (or value in regression problems) is multiplied are proportional to the inverse of the distance between that point and the point for which the class is to be predicted also significantly improves the results.

See also

• Nearest neighbor search
• Cluster analysis
• Data classification
• Data mining
• Machine learning
• Pattern recognition
• Predictive analytics
• Dimension reduction

References

Further reading

• When Is "Nearest Neighbor" Meaningful?
• Belur V. Dasarathy, ed. (1991). Nearest Neighbor (NN) Norms: NN Pattern Classification Techniques.