FreeEnergyLesson4

LESSON 4: TEMPERATURE DEPENDENCE OF GIBBS ENERGY

The temperature dependence of Gibbs energy, (G/T)_p = -S, was given by eq (3.5). For a chaemical reaction with all species in the standard state we can write:

d∆_IG^o/dT = -∆_IS^o (4.1)

since ∆_IG^o implies that all reactants and products are at standard pressure.

From the two expressions for ∆_IG^o:

∆_IG^o = ∆_IH^o - T∆_IS^o from eq.(2.1)

and:

∆_IG^o = -RT ln K from eq.(3.17)

we shall derive a relationship between ∆_IH^o and In K. Differentiating eq. (3.17) with respect to

T and changing signs we obtain:

∆S^o = R In K + RT dIn K/dT

Multiplying with T, and replacing RT In K with ∆_IG^o, give:

T∆_IS^o = -∆_IG^o + RT² dIn K/dT

Using eq. (2.1) and rearranging, we obtain:

d ln K/dT = ∆_TH^o/RT² (4.2)

This equation is often called the van t'Hoff equation.

Since d ln K = - dT/T², eq. (4.2) can be given the form:

d ln K/d(l/T) = -∆_TH^o/R(4.3)

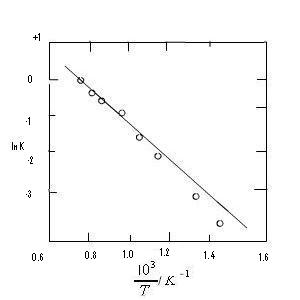
When plotting In K as a function of VT we obtain -∆_rH^o/R as the slope of the curve, see Fig. 4.1. The variation in ∆_rH^o with temperature is given by eq (5.9)in 1st law of thermodynamics lesson 5

∆rHoT = ∆rHo298 + ∆rCPodT 

∆_rH^o_T = ∆_rH^o₂₉₈ + ∆_rC_p^odT

The integral in the eq. ∆_rH^o_T = ∆_rH^o₂₉₈ + ∆_rC_p^odT will usually have a small value compared to ∆_rH^o₂₉₈ except when the temperature range is very large. This means that the curve in Fig. 4.1 is approximately a straight line. ∆_rH^o for a reaction is found from a plot similar to the one in Fig. 4.1. The experiment shows that the variation in ∆_rH^o with temperature can be ignored.

Fig. 4.1. The temperature dependence of the equilibrium constant for the reaction: CO₂(g) + H₂ (g) = CO (g) + H₂O (g).

The variation with temperature of ∆_rS^o for a reaction is also usually very small, and therefore ∆_rG^o for a reaction is usually a practically linear function of temperature. For many purposes one will obtain results with sufficient accuracy by replacing the equation:

∆_rG^o_T = ∆_rH^o_T - T∆_rSO_T

with the approximate equation:

∆_rG^o_T = ∆_rH^o₂₉₈ - T∆_rS^o₂₉₈ (4.4)

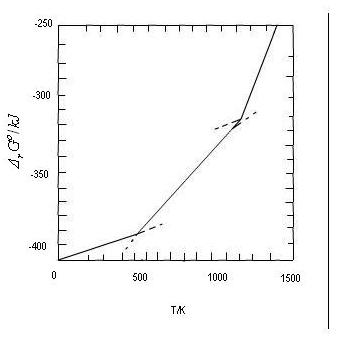
Equation (6.45) represents a straight line with the slope ∆_rS^o₂₉₈. If the line is extrapolated to the absolute zero, the intercept with the ordinate gives ∆_rH^o₂₉₈ At temperatures of transition, there is a change in ∆_rH^o and a corresponding change in ∆_rS^o.

Equation (4.8)in Entropy lesson 4, gives the relation between ∆_fusS^o and ∆_fusH^o at the melting point. When a transition takes place reversibly, i.e., the system and the surroundings are at the same temperature, the transition temperature, there is no change in ∆_rG^o. There is a break in the curve for ∆_sG^o as a function of T, however, since the values of ∆_rH^o and ∆_rS^o have changed by the transition. An increased slope corresponds to a phase transition in a reactant, whereas a decreased slope corresponds to a phase transition in a product. The change in slope corresponds to the entropy of transition. It is small for melting and large for boiling.

Example1

We shall calculate ∆_rG^o for NaCl as a function of temperature in the range 298 - 1400 K using the approximate eq. (4.4)

Table4.1 NaCl as a function of temperature

In a temperature range where there is no phase change we assume constant values for ∆_fH^o and ∆_fS^o. A phase change leads to changes in ∆_fH^o and ∆_fS^o.

Temperature range 298 - 371 K: Na (s) + 112 Cl2 (g) = NaCI (s)

∆_fH^o = - 411 kI, ∆_fS^o = 72 - 51 - 112x223 = - 90.5 I K^-1 (see eq. 2.2)

∆_fG^o = (- 411 + T 90.5/1000) kJ

Temperature 371 K: Na (s) = Na (1); ∆_fusH/T_fus = 3000/371 = 8 I K-l = ∆_fusS (see eq. (4.8)in Entropy lesson 4)

∆_fusG = ∆_fusH - T_fus∆_fusS = 0

Temperature range 371 - 1074 K: Na (I) + 1/2 Cl₂ (g) = NaCI (s)

∆_fH^o = - 411 - 3 = - 414 kJ; ∆_fS^o = - 90.5 - 8 = - 98.5 J K^-1

∆_fG^o = (-414 + T 98.5/1000) kJ

Temperature 1074 K: NaCl (s) = NaCl (l); _fusH/T_fus = 28000/1074 = 26.1 J K_-1 = ∆_fS

∆_fusG = 0

Temperature range 1074 - 1165 K: Na (I) + 1/2 Cl₂ (g) = NaCl (I)

∆_fH^o = - 414 + 28 = - 386 kJ; ∆_fS^o =- 98.5 + 26.1 = - 72.4 J K^-1

∆_fG^o = (-386 + T 72.4/1000) kJ

Temperature 1165 K: Na (l) = Na (g); ∆_vapH/lT_b = 106000/1165 = 91 J K^-1 = ∆_vapS = 0

∆_vapG =0

Temperature range 1165 - 1400 K: Na (g) + 1/2 Cl₂ (g) = NaCI (I)

∆_fH^o - 386 - 106 - = - 492 kJ; ∆_fS^o = - 72.4 - 91 = - 163.4 J K^-1

∆_fG^o = (-492 + T 163.4/1000) kJ

Fig. 4.2 The Gibbs energy of formation for one mole NaCI as a function of temperature