EntropyLesson4

LESSON 4; ENTROPY IN CHEMICAL THERMODYNAMICS

1.1 TITLE : ENTROPY CALCULATIONS FOR REVERSIBLE AND IRREVERSIBLE CHANGES

LEARNING OUTCOMES:

The student should , at the end of the lesson , be able

• To carry out calculations for both reversible and irreversible processes
• To create reversible paths for irreversible processes

LESSON DEVELOPMENT

In order to calculate the change in entropywhen a system goes from one state a, to another b, we have to find a reversible path from a to b, and then calculate the integral:

S_b - S_a = ∆S = dq_rev/T (4.1)

Since ∆S is a state function, any path will do as long as it is reversible. Since we are at liberty choosing the reversible path, it is convinient to choose a path that gives an easy integration.

From the isothermal expansion for an ideal gas from V₁ to V₂, we have:

∆S = q_rev/T = R X Image:V1IntegralV2.jpgdV/V = R ln(V₂/V₁)

We can therefore express the entropy change by means of the pressures:

∆S = q_rev = R ln V₂/V₁ = R ln P₁/P₂ = - R ln P₂/P₁ (4.2)

At moderate pressures (about 1 bar) and not too low temperatures, only a small error is introduced when treating a real gas as an ideal gas. The entropy of a liquid or a solid changes very little with pressure, and usually this entropy change may be ignored.

When heating a substance at constant pressure, only pressure - volume work being carried out, we have dq_rev = dH = C_pdT. This gives:

∆S = q_rev/T = C_p dT/T (4.3)

Thus when C_p as a function of T is known, we can calculate ∆S. In many cases C_p may be considered a constant over a reasonably small temperature interval, and then the integration will give:

∆S = C_p ln (T₂/T₁) (4.4)

At constant volume:

∆S = C_v ln (T₂/T₁) (4.5)

For melting, vaporization or any transition of a substance from one equilibrium state to another at constant temperature and pressure, the change in entropy for the system is:

∆_trsS = q_rev/T_trs = ∆_trsH/T_trs (4.6)

where T_trs is the transition temperature and ∆_trsH is the change in ethalpy for the transition at equilibrium temperature.

If we want to calculate the change in entropy when a system goes from one state to another involving phase transitions, temperature change and pressure change, the calculation may be facilitated by considering the change taking place in the following reversible steps: transition at the equilibrium temperature, changing temperature at constant pressure and changing pressure at constant temperature. The number of steps may be chosen to give the most convinient calculation so long as all steps are reversible.

Example 1

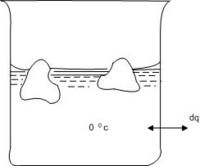
Consider the melting of ice at 0^oC where we have equilibrium between ice and liquid water. Thus the melting may take place under practically reversible conditions as shown in Fig 4.1.

Fig.4.1 Reversible melting of ice

A beaker containing ice and water is placed in a thermostat at 0^oC. Heat is added to the thermostat in infinitesimal amounts. The added heat is absorbed by the system ice-water in the beaker, melting some of the ice, keeping the temperature constant at0^oC.

Since the process is taking place at constant pressure (atmospheric pressure), with only pressure - volume work performed, the heat absorbed upon melting one mole of ice is equal to the enthalpy of melting per mole, ∆_fusH₂₇₃:

H₂O(s) + H₂O(l) = 6010J (4.7)

Since the process is carried out reversibly, the heat absorbed is equal to q_rev at the melting point, T_fus = 273 K. We have the change in entropy for the process

∆_fusS = ∫dq_rev/T_fus = q_rev/T_fus = ∆_fusH/T_fus 6010/273 = 22.0 J K^-1 mol^-1 (4.8)

where ∆_fusS is the entropy of melting per mole ice, while ∆_fusH is the enthalpy of melting per mole ice.

When the system absorbs a heat, q_rev, the surroundings must donate the same amount of heat. Expressed in a different way, the heat absorbed by the surroundings i equal to -q_rev. There will be an entropy change also in the surroundings, ∆S_sur. For a reversible process, i.e, the temperature is the same for system and surroundings, the total entropy change is equal to zero.

∆S_total = ∆S_system + ∆S_sur = 0 (4.9)

If the process is irreversible, the change in entropy for the system is the same. The entropy change for the system can be calculated choosing a reversible path. The entropy change for the surroundings, however, will be different when the process is irreversible.

The melting point of ice at 0^oC, studied in example 1, is a reversible process. If the is placed in water of a temperature higher than 0^oC, it melts irreversibly.

Example 2

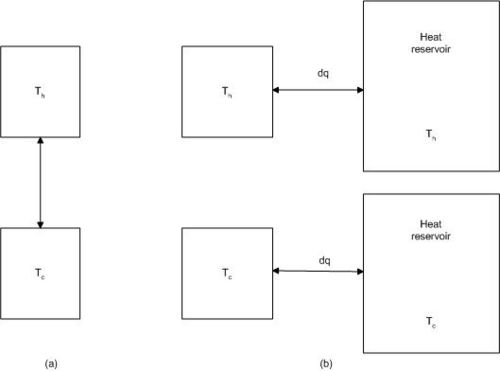
We now consider a system consisting of two subsystems at different temperatures.The two subsystems may be two pieces of metal, one at T_h (hot) and one at T_c (cold). We can bring the two pieces in contact for a short time, and a small amount heat, dq, is transferred irreversibly from the hot to the cold metal. No heat is lost to the surroundings.

In order to derive an expression for the entropy change for the system, we find a reversible path for transferring the heat dq, bringing the system from the initial state to the final state.

The process can be carried out in a reversible way when we bring the hot subsystem in contact with a reservoir at a temperature infinitesimally lower than T_h, and the cold subsystem in contact with a reservoir at a temperature infinitesimally higher than T_c.

Fig. 4.2 Irreversible (a) and reversible (b) transfer of heat

The entropy change for the system is the sum of the entropy changes for ,the two subsystems:

∆S_sytem = -dq/T_h + dq/T_c > 0

The ∆S system is the same for the irreversible and the reversible process, since the initial and final states are the same. In the reversible case we also have changes in the reservoirs:

∆S_sur = dq/T_h – dq/T_c < 0

If the temperature differences between subsystems and reservoirs are infinitesimally the small we have:

∆S_system + ∆S_sur = 0

In the irreversible case the heat was transferred directly between the subsystems. There was no heat reservoir and no heat leaked to the surroundings, hence ∆S_sur = 0

For the reversible process we have: ∆S _total = 0 (4.10)

For the irreversible process we have: ∆S_total > 0 (4.11)

Example 3

Isothermal expansion of an ideal gas.

For the reversible isothermal expansion of one mole ideal gas we have found q_system =RT ln( V₂/V₁) and ∆S_sytem =R In ( V₂/V₁) To keep the temperature constant heat must be supplied from a heat reservoir at the same temperature, q_sur = RT In (V₂/V₁) and then ∆S_surr=-R In (V₂ /V₁). Hence we have

∆S_total = ∆S_sytem + ∆S_sur = 0

If no work is performed by the expansion, i.e., the expansion takes place irreversibly, such as in Joule's experiment then no heat is absorbed by the surroundings, ∆S_sur = 0 The total entropy change is:

∆S_total = ∆S_sytem + 0 = R In ( V₂/V₁) > 0

Example 4

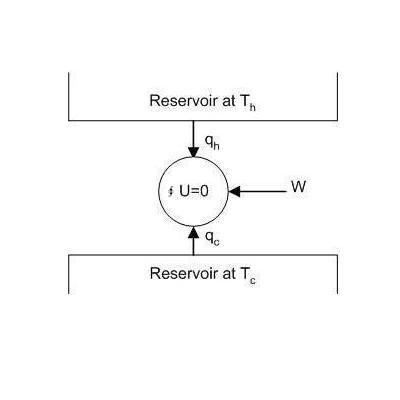
The General Case We shall now consider a system in contact with two heat reservoirs at the temperature T_h and T_c respectively, as shown in Fig. 4.3. The system is unspecified, it may be of any kind. The system is going through a cyclic process.

Fig. 4.3A cyclic process going through states at T_h and T_C'

For a cyclic process ∮dU = 0 and from the first law we have:

q_h + q_c+ w = 0

From the second law we have for the cyclic process:

∮dS = ∆S_system = q_h/T_h + q_c/T_c

If the process is reversible, the efficiency is -w_rev/q_h, and the entropy change in the surroundings (the reservoirs) is:

∆S_sur = -q_h/T_h +-q_c/T_c = 0

and

∆S_total = ∆S_system + ∆S_sur = 0 (4.12)

If the process is irreversible, the efficiency is lower, less work is taken out of the system for the same value of q_h, -w_ir/q_h < -w_rev/q_h This means that more heat is supplied to the reservoir at T_c, and its entropy will increase more than it does in the reversible case. For the entropy of the surroundings we have:

∆S_sur = -q_h/T_h + -q_c,ir/T_c > 0

The entropy change of the system is the same for the reversible and the irreversible process. Hence, for the irreversible process we have:

∆S_total = ∆S_system + ∆S_sur > 0

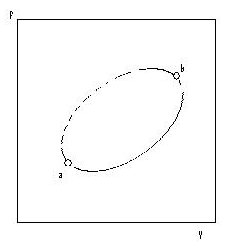
Next we shall consider an irreversible non-cyclic process from a to b, see Fig 4.4. We can make the process cyclic by adding a reversible process from b to a.

Fig. 4.4 An irreversible process, a to b, combined w ,a reversible process, b to a, to form a cycle

Fig. 4.4 An irreversible process, a to b, combined w ,a reversible process, b to a, to form a cycle When a part of a cyclic process is irreversible, the whole cycle is irreversible, and the total entropy change is positive:

∆S_total,cycle = ∆S_a→b + ∆S_b→a > 0

For the reversible part of the cycle the entropy change is equal to zero:

∆S_total,b→a = 0