EntropyLesson3
Contents
[hide]LESSON 3: Entropy and Disorder
Interpretation of Entropy and Calculation
Learning Objectives
After the study of this topic learners should be able to:
- Describe how entropy is related to randomness or disorder
- Predict for certain processes whether entropy increases or decreases. Predict whether the entropy change in a given process is positive or negative or zero
- State the second law of thermodynamics
- State the third law of thermodynamics and to explain how it makes possible an evaluation of absolute entropies of substances
- Describe how and why the entropy of a substance changes with increasing temperature or when a phase change occurs starting with the substance as a pure solid at OK
Calculate ∆So for any reaction from tabulated absolute entropy values So
Introduction
We have now seen several examples of processes that occur spontaneously, some exothermic and some endothermic. In order to understand why spontaneous processes occur, let us consider the expansion of a gas into a vacuum at molecular level.
- Consider the expansion of an ideal gas
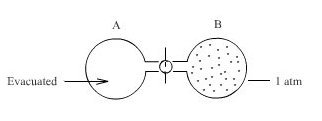
- Consider Initial State, two 1 litre flasks connected by a closed stopcock, one flask is evacuated and the other containing 1 atm of gas
We open the stopcock while maintaining the system at constant temperature(isothermal), what would you expect to happen?
We know that the molecule of a gas are in constant motion and that they will move in to whatever space is available to them - gases expand to fill their containers.
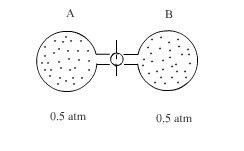
The ideal gas expands spontaneously to occupy both flasks Aand B at a pressure of 0.5 atmosphere. Since this process is spontaneous, we might next enquire as to what property of the system has undergone a change.
During this constant temperature(isothermal) expansion into vacuum, the gas does no work (w=0)
Furthermore, because the internal energy and enthalpy of an ideal gas depends only on temperature and not on the gas volume or pressure which is constant during the process ∆E = 0 for the expansion. For the mixing of gases at constant temperature
∆E = ∆H = 0 (3.1)
The product Pv is the internal energy of an ideal gas. For an ideal gas Pv = nRt. If T is constant nRt is constant. The energy of the gas is therefore constant, so fo a change occurring at constant pressure ∆E = 0
One characteristic of the above system, however is greatly altered by the mixing process. The degree of order that prevails. In the initial condition of the above figure there is some degree of order at least to the extent that all the molecules of a gas are
Relating Entropy to Heat transfer
We can relate the change in entropy to other familiar thermodynamics quantities especially the way it is related to heat transferred during the process. As explained earlier, entropy is a state function. however in order to understand the relationship between change in entropy and heat, we need to remember that heat is not a state function.suppose a system undergoes a process in which it changes from an initial state say state1 to a final state say state2. The heat transferred during the process,q, depends on the path we take from from state 1 to state2. To relate dS to heat q we need to consider a particular path from state 1 to state 2, namely a reversible path
At the end of the lesson the students should :
Entropy is studied under the second law of thermodynamics . An important part of chemistry is concerned with the state of equilibrium and the tendency of a system to move in the direction of equilibrium . The second law is concerned with the direction of spontaneous reactions and with equilibrium. Since both exothermic and endothermic reactions may proceed spontaneously, the driving force of a chemical reaction cannot be explained by the change of enthalpy alone. A process that occurs spontaneously involves a change of lower probability to a state of higher probability.
Before attempting this lesson students should be familiar with some language of thermodynamics which you learnt earlier on in the First Law of Thermodynamics.
- Closed system
- Open system
- Isolated system
- Universe
- Surroundings
- State function
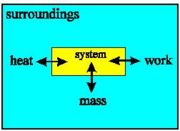
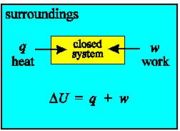
With a closed system, no transfer of mass is possible: internal energy may only change due to heat and work.
With an isolated system, no change in the internal energy is possible: heat, work and mass transfer are all impossible.
With an open system, the internal energy may change due to transfer of heat, mass and work between system and surroundings.
The System and The Surroundings
Because we are interested in the heat given off by reactions it is very important to define the system that we are studying. In this way we can be sure exactly what we mean when we say, for example, that so many joules of heat have been given off - this amount of heat energy has left the system.
Note that the system may be defined by physical boundaries, like a test-tube or a bomb calorimeter, or the system may simply be defined by a set of cartesian coordinates specifying a particular volume in space.
Once we've defined the system as the particular region of space that we are making measurements on, the definition of the surroundings follows naturally - the surroundings are everything that is not the system.
One way of summarizing what we have just said:
The Universe = The System + The Surroundings (3.2)