EntropyLesson2

Lesson Outcomes

By the end of the lesson each student should be able to:

• Show and proof that entropy is a state function.
• Carry out calculations for changes of entropy in both reversible and irreversible changes.
• Describe heat changes that take place in a Carnot engine

Introduction:

In the last lesson we explored the concept of entropy and developed a method of calculation of change of entropy during the isothermal expansion of an ideal gas. One issue that was raised and not fully settled was the proof to show that entropy is a state function that depends on the initial and final parameters that describe the system.

In this lesson we shall cover the Carnot Engine Cycle to show that the total change of Entropy in a cyclic process in equal to zero and hence entropy is a state function just like internal energy Uand enthalpy H

The Carnot Cycle

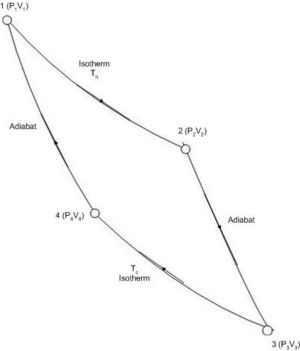
In the Carnot cycle we expose one mole of an ideal gas to reversible isothermal and adiabatic processes. The gas is placed in a cylinder with a piston. A pressure – volume diagram for the Carnot cycle is shown below

Fig. 2.1 The Carnot cycle

Initially, in state 1, the pressure of the gas is P₁ and its volume is V₁ The temperature of the gas is T_h (where h stands for hot ).

We shall bring about four reversible changes in the system to complete a cycle bringing it back to state 1.

• Step 1→2: Reversible isothermal expansion of the gas to state 2, where pressure is P₂ and volume is V₂. Temperature is T_h

• Step 2→3: Reversible adiabatic expansion of the gas to state 3, where pressure is P₃ and volume is V₃. In the adiabatic expansion the temperature of the gas has decreased to T_c (c for cold).

• Step 3→4: Reversible isothermal compression of the gas at T_c to state 4, where pressure is P₄ and volume is V₄.

• Step 4→1: Reversible adiabatic compression of the gas to return to state 1.

For the two isothermal processes we have ∆U = 0 for an ideal gas, and q_rev = - w. For the two adiabatic processes we have q_rev = 0 and w_rev = ∆U = C_v∆T. (For an ideal monatomic gas C_v does not change with temperature). The reversible work and heat for an isothermal process are obtained using eq. (1.6). The work and change in internal energy for an adiabatic process are obtained using eq.(1.31). The expressions for the four steps of the cyclic process are shown in Table 2.1. Table 2.1. Expressions for ∆U, q_rev and w_rev for the four steps of the Carnot cycle.

Table 2.1 Expressions for the cyclic process

From the equation for the reversible adiabatic expansion Of an ideal gas, eq.(1.28) we have for the step 2→3:

V₂/V₃ = (T_c/T_h)^C_v/R

or

V₂T_h^C_v/R = V₃T_c^C_v/R (2.1)

In a similar way we obtain for the step 4-1:

V₁T_h^C_v/R = V₄T_c^C_v/R (2.2)

From eqs (2.1), 2.2) we obtain:

V₂/V₁ = V₃/V₄ (2.3)

From the expressions for q_rev in Table 2.1 and eq.(2.3) we obtain for the whole cycle:

∑q_rev/T = q_1-2/T_h + q_3-4/T_c = Rln(V₂/V₁) + Rln(V₄/V₃) = 0 (2.4)

For the entropy change for the whole cycle we obtain:

∑∆S = ∑q_rev/T = 0 (2.5)

This is in agreement with the requirement for a state function. By the first law we have for the complete Carnot cycle:

∑∆U = 0 = ∑q_rev + ∑w_rev (2.6)

The efficiency of the reversible Carnot engine can be defined as the ratio of the work done on the surroundings to the heat input at the higher temperature.

Efficiency: η = -w/q_h = R(T_h-T_c)ln(V₂/V₁)/RT_hln(V₂/V₁) = T_h-T_c/T_h = q_h + q_c/q_h (2.7)

As a next step we shall investigate if eq. (2.5) is valid for any kind of system, e.g. a non-ideal gas, liquid, solid or a mixture of these.

Entropy Changes for an Arbitrary System going through a Reversible Cyclic Process

The second law of thermodynamics may be stated in different ways. Here we shall use the statement by Clausius (1856): It is impossible to transfer heat from a cold reservoir to a hot one without at the same time converting an amount of work into heat. The second law is a postulate, it cannot be derived, but it is in accordance with our experience, that heat never flows spontaneously from a cold to a hot body. To obtain the entropy change for an arbitrary system we compare the changes in this system with those in the system of an ideal gas. Let us assume that we have two reversible Carnot engines working between the same two heat reservoirs at T_b and T_c. The engines are adjusted to perform equal amounts of work in a cycle. Suppose that the engines are of different efficiency, and arranged such that the more efficient engine,A, operates the less efficient engine, B, in reverse with no extra energy available. The engine operated in reverse takes heat from the cold reservoir to the hot reservoir. If engine B were less efficient,-w/q_h,B < -w/q_h,A or q_h,B > w/q_h,A, more heat would be transferred from the cold reservoir to the hot reservoir by engine B, than the heat transferred in the opposite direction by engine A. The net result would be the transfer of heat from the cold reservoir to the hot one without converting any work into heat. This violates the second law as stated by Clausius, although the first law is not violated. Thus, the efficiency of any reversible Carnot engine must be the same as that for the ideal gas reversible Carnot engine. Hence, for any kind of system the reversible Carnot cycle gives ∑(q_rev/T) = ∑∆S = 0, according to eq. (2.5). Notice that ∑q_rev is not equal to zero, since q_rev is not a state function.

The General cycle

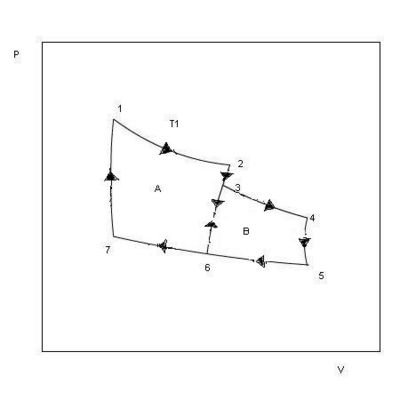
If the entropy is a state function, we must have ∑∆S = 0 for any cycle of reversible processes. The Carnot cycle consists of two reversible isothermal parts and two reversible adiabatic parts. For a cycle that consists of several distinct reversible isothermal and adiabatic parts, the entropy change will be equal to zero. We shall first consider a cycle where the system goes through three different temperatures as shown in Fig. 2.2. The cyclic process, 1→2→3→4→5→6→7→1, goes through states at three different temperatures, T₁, T₂, T₃, and it consists of reversible isothermal and adiabatic parts. From the figure we see that the process is equal to the sum of process A(1→2→6→7→1) and process B(3→4→5→6→3). Between 3 and 6 the changes in process A and process B cancel. Each one of the processes A and B is a Carnot cycle where

∑∆S = ∑((q_rev/T) = O. The same must be true for the sum of the two processes, A + B.

Fig. 2.2. A cyclic process consisting of reversible isothermal and adiabatic processes

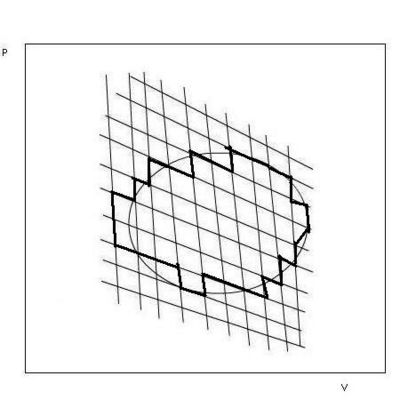
This procedure of adding two Carnot cycles can be extended to a large number. The entropy change for each cycle is zero, and the sum of all the cyclic processes is equal to a cyclic process described by the boundary line framing the cycles, see Fig. 2.3. All processes inside the boundary cancel, and the process described by the boundary line consists of reversible isothermal and adiabatic processes. In principle we can approach an arbitrary, reversible or irreversible cyclic process as closely as we wish by small steps consisting of reversible isothermal and adiabatic processes. The sum of the small steps over the whole cycle is equal to the sum of small reversible cyclic processes, each having ∑∆S = O. Thus, for any cyclic process for any kind of system we have:

∮ dq_rev/T = ∮dS = 0 (2.8) The entropy is a state function.

Fig. 2.3 An arbitrary cyclic process, reversible or irreversible, is approached by a sum of reversible isothermal and adiabatic processes