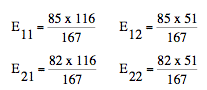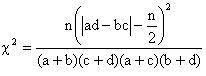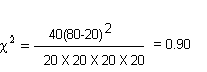Educational Statistics
Contents
Correlation
Purpose (What is Correlation?)
Correlation is a statistical technique to measure the relation between two or more variables. It can show whether and how strongly pairs of variables are related. For example, height and weight are related; taller people tend to be heavier than shorter people. The relationship isn't perfect. People of the same height vary in weight, and you can easily think of two people you know where the shorter one is heavier than the taller one. Nonetheless, the average weight of people 5'5 is less than the average weight of people 5'6, and their average weight is less than that of people 5'7, etc. Correlation can tell you just how much of the variation in peoples' weights is related to their heights. The measurement scales used should be at least interval scales, but other correlation coefficients are available to handle other types of data.
Correlation Coefficient
The main result of a correlation is called the correlation coefficient (or "r"). It ranges from -1.0 to +1.0. The closer r is to +1 or -1, the more closely the two variables are related. The value of -1.00 represents a perfect negative correlation while a value of +1.00 represents a perfect positive correlation. A value of 0.00 represents a lack of correlation.
If r is close to 0, it means there is no relationship between the variables. If r is positive, it means that as one variable gets larger the other gets larger. If r is negative it means that as one gets larger, the other gets smaller (often called an "inverse" correlation).
http://www.statsoft.com/textbook/elementary-concepts-in-statistics/
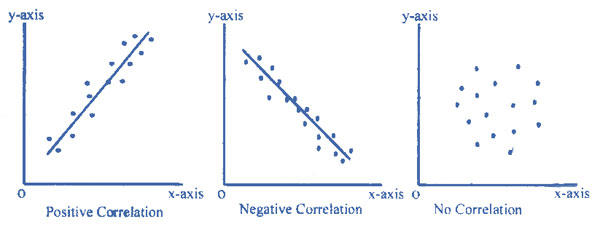
Types of Correlation
- Positive Correlation:
The correlation in the same direction is called positive correlation. If one variable increase other is also increase and one variable decrease other is also decrease. For example, the length of an iron bar will increase as the temperature increases.
- Negative Correlation:
The correlation in opposite direction is called negative correlation, if one variable is increase other is decrease and vice versa, for example, the volume of gas will decrease as the pressure increase or the demand of a particular commodity is increase as price of such commodity is decrease.
- No Correlation or Zero Correlation:
If there is no relationship between the two variables such that the value of one variable change and the other variable remain constant is called no or zero correlation.
Spearman's rank correlation coefficient
http://en.wikipedia.org/wiki/Spearman%27s_rank_correlation_coefficient
Inferential Statistics (Non-Parametric)
What Does Nonparametric Statistics Mean?
Before discussing nonparametric techniques, we should consider why the methods we usually use are called parametric. Parameters are indices. They index (or label) individual distributions within a particular family. For example, there are an infinite number of normal distributions, but each normal distribution is uniquely determined by its mean and standard deviation. If you specify all of the parameters (here, mean and SD), you've specified a unique normal distribution.
Most commonly used statistical techniques are properly called parametric because they involve estimating or testing the value(s) of parameter(s)--usually, population means or proportions. It should come as no surprise, then, that nonparametric methods are procedures that work their magic without reference to specific parameters.
- A statistical method wherein the data is not required to fit a normal distribution. Nonparametric statistics uses data that is often ordinal, meaning it does not rely on numbers, but rather a ranking or order of sorts. For example, a survey conveying consumer preferences ranging from like to dislike would be considered ordinal data.
Nonparametric statistics have gained appreciation due to their ease of use. As the need for parameters is relieved, the data becomes more applicable to a larger variety of tests. This type of statistics can be used without the mean, sample size, standard deviation, or the estimation of any other related parameters when none of that information is available.
Scope and use of Nonparametric Statistics in Education
Non-parametric methods are widely used for studying populations that take on a ranked order (such as movie reviews receiving one to four stars). The use of non-parametric methods may be necessary when data have a ranking but no clear numerical interpretation, such as when assessing preferences; in terms of levels of measurement, for data on an ordinal scale.
As non-parametric methods make fewer assumptions, their applicability is much wider than the corresponding parametric methods. In particular, they may be applied in situations where less is known about the application in question. Also, due to the reliance on fewer assumptions, non-parametric methods are more robust.
Another justification for the use of non-parametric methods is simplicity. In certain cases, even when the use of parametric methods is justified, non-parametric methods may be easier to use. Due both to this simplicity and to their greater robustness, non-parametric methods are seen by some statisticians as leaving less room for improper use and misunderstanding.
The wider applicability and increased robustness of non-parametric tests comes at a cost: in cases where a parametric test would be appropriate, non-parametric tests have less power. In other words, a larger sample size can be required to draw conclusions with the same degree of confidence.
Rationale for distribution free data
A method commonly used in statistics to model and analyze ordinal or nominal data with small sample sizes. Unlike parametric models, nonparametric models do not require the modeler to make any assumptions about the distribution of the population, and so are sometimes referred to as a distribution-free method.
Typically, this method will be used when the data has an unknown distribution, is non-normal, or has a sample size so small that the central limit theorem can't be applied to assume the distribution.
Rationale and use of Nonparametric hypothesis testing
Nonparametric, or distribution free tests are so-called because the assumptions underlying their use are “fewer and weaker than those associated with parametric tests” (Siegel & Castellan, 1988, p. 34). To put it another way, nonparametric tests require few if any assumptions about the shapes of the underlying population distributions. For this reason, they are often used in place of parametric tests if/when one feels that the assumptions of the parametric test have been too grossly violated (e.g., if the distributions are too severely skewed).
Chi-Square Test in mXn Contingency Table
Contingency tables are used to examine the relationship between subjects' scores on two qualitative or categorical variables. For example, consider the hypothetical experiment on the effectiveness of early childhood intervention programs described in another section. In the experimental group, 73 of 85 students graduated from high school. In the control group, only 43 of 82 students graduated. These data are depicted in the contingency table shown below.
| Graduated | Failed to Graduate | Total | |
|---|---|---|---|
| Experimental | 73 | 12 | 85 |
| Control | 43 | 39 | 82 |
| Total | 116 | 51 | 167 |
The cell entries are cell frequencies. The top left cell with a "73" in it means that 73 subjects in the experimental condition went on to graduate from high school; 12 subjects in the experimental condition did not. The table shows that subjects in the experimental condition were more likely to graduate than were subjects in the control condition. Thus, the column a subject is in (graduated or failed to graduate) is contingent upon (depends on) the row the subject is in (experimental or control condition).
If the columns are not contingent on the rows, then the rows and column frequencies are independent. The test of whether the columns are contingent on the rows is called the chi square test of independence. The null hypothesis is that there is no relationship between row and column frequencies.
The first step in computing the chi square test of independence is to compute the expected frequency for each cell under the assumption that the null hypothesis is true. To calculate the expected frequency of the first cell in the example (experimental condition, graduated), first calculate the proportion of subjects that graduated without considering the condition they were in. The table below shows that of the 167 subjects in the experiment, 116 graduated.
| Graduated | Failed to Graduate | Total | |
|---|---|---|---|
| Experimental | 73 | 12 | 85 |
| Control | 43 | 39 | 82 |
| Total | 116 | 51 | 167 |
Therefore, 116/167 graduated. If the null hypothesis were true, the expected frequency for the first cell would equal the product of the number of people in the experimental condition (85) and the proportion of people graduating (116/167). This is equal to (85)(116)/167 = 59.042. Therefore, the expected frequency for this cell is 59.042. The general formula for expected cell frequencies is:
where Eij is the expected frequency for the cell in the ith row and the jth column, Ti is the total number of subjects in the ith row, Tj is the total number of subjects in the jth column, and N is the total number of subjects in the whole table.
The calculations are shown below.
Once the expected cell frequencies are computed, it is convenient to enter them into the original table as shown below. The expected frequencies are in parentheses.
| Graduated | Failed to Graduate | Total | |
|---|---|---|---|
| Experimental | 73
(59.042) |
12
(25.958) |
85 |
| Control | 43
(56.958) |
39
(25.042) |
82 |
| Total | 116 | 51 | 167 |
The formula for chi square test for independence is
For this example,
χ² = 22.01
The degrees of freedom are equal to (R-1)(C-1) where R is the number of rows and C is the number of columns. In this example, R = 2 and C = 2, so df = (2-1)(2-1) = 1. A chi square table can be used to determine that for df = 1, a chi square of 22.01 has a probability value less than 0.0001.
In a table with two rows and two columns, the chi square test of independence is equivalent to a test of the difference between two sample proportions. In this example, the question is whether the proportion graduating from high school differs as a function of condition. Whenever the degrees of freedom equal one (as they do when R = 2 and C = 2), chi square is equal to z². Note that the test of the difference between proportions for these data results in a z of 4.69 which, when squared, equals 22.01.
The same procedures are used for analyses with more than two rows and/or more than two columns. For example, consider the following hypothetical experiment: A drug that decreases anxiety is given to one group of subjects before they attempted to play a game of chess against a computer. The control group was given a placebo. The contingency table is shown below.
| Condition | Win | Lose | Draw | Total |
|---|---|---|---|---|
| Drug | 12
(14.29) |
18
(14.29) |
10
(11.43) |
40 |
| Placebo | 13
(10.71) |
7
(10.71) |
10
(8.57) |
30 |
| Total | 25 | 25 | 20 | 70 |
The expected frequencies are shown in parentheses. As in the previous example, each expected frequency is computed by multiplying the row total by the column total and dividing by the total number of subjects. For example, the expected frequency for the "Drug-Lose" condition is the product of the row total (40) and the column total (25) divided by the total number of subjects (70): (40)(25)/70 = 14.29.
The chi square is calculated using the formula:
The df are (R-1)(C-1) = (2-1)(3-1) = 2. A chi square table shows that the probability of a chi square of 3.52 with 2 degrees of freedom is 0.172. Therefore, the effect of the drug is not significant.
Summary of Computations
- Create a table of cell frequencies.
- Compute row and column totals.
- Compute expected cell frequencies using the formula:
where Eij is the expected frequency for the cell in the ith row and the jth column, Ti is the total number of subjects in the ith row, Tj is the total number of subjects in the jth column, and N is the total number of subjects in the whole table.
- Compute Chi Square using the formula:
- Compute the degrees of freedom using the formula: df = (R-1)(C-1) where R is the number of rows and C is the number of columns.
- Use a chi square table to look up the probability value.
Median Test
Median test is used for testing whether two groups differ in their median value. In simple terms, median test will focus on whether the two groups come from populations with the same median. This test stipulates the measurement scale is at least ordinal and the samples are independent (not necessary of the same sample size). The null hypothesis structured is that the two populations have the same median. Let us take an example to appreciate how this test is useful in a typical practical situation.
Example: A private bank is interested in finding out whether the customers belonging to two groups differ in their satisfaction level. The two groups are customers belonging to current account holders and savings account holders. A random sample of 20 customers of each category was interviewed regarding their perceptions of the bank's service quality using a Likert-type (ordinal scale) statements. A score of "1" represents very dissatisfied and a score of "5" represents very satisfied. The compiled aggregate scores for each respondent in each group are tabulated be given below:
| Current Account | Saving Account |
|---|---|
| 79 | 85 |
| 86 | 80 |
| 40 | 50 |
| 50 | 55 |
| 75 | 65 |
| 38 | 50 |
| 70 | 63 |
| 73 | 75 |
| 86 | 80 |
| 50 | 55 |
| 40 | 45 |
| 20 | 30 |
| 80 | 85 |
| 55 | 65 |
| 61 | 80 |
| 50 | 55 |
| 80 | 75 |
| 60 | 65 |
| 30 | 50 |
| 70 | 75 |
| 50 | 62 |
What are your conclusions regarding the satisfaction level of these two groups?
Analysis and Interpretations:
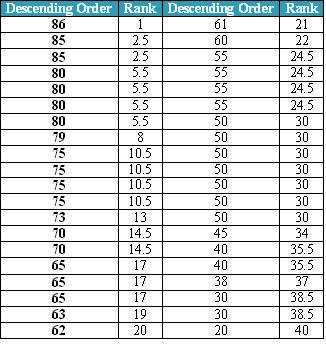
The first task in the median test is to obtain the grand median. Arrange the combined data of both the groups in the descending order of magnitude. That is rank them from the highest to the lowest. Select the middle most observation in the ranked data. In this case, median is the average of 20th and 21st observation in the array that has been arranged in the descending order of magnitude.
Table showing descending order of aggregate score and rank in the combined sample
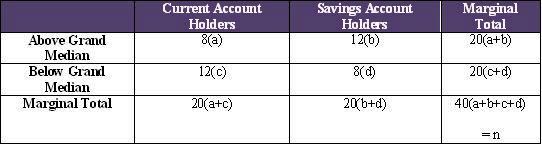
Grand median is the average of 20th and 21st observation = (62+61)/2 =61.5. Please note that in the above table, average rank is taken whenever the scores are tied. The next step is to prepare a contingency table of two rows and two columns. The cells represent the number of observations that are above and below the grand median in each group. Whenever some observations in each group coincide with the median value, the accepted practice is to first count the observations that are strictly above grand median and put the rest under below grand median. In other words, below grand median in such cases would include less than or equal to grand median.
Scores of Current Account Holders and Savings Account Holders as compared with Grand Median
Null Hypothesis: There is no difference between the current account holders and savings account holders in the perceived satisfaction level.
alternative Hypothesis: There is difference between the current account holders and savings account holders in the perceived satisfaction level.
The test statistic to be used is given by
on substituting the values of a, b, c, d, and n we have
Critical chi-square for 1 d.f at 5% level of significance = 3.84 (click here for the table). Since the computed chi-square(0.90) is less than critical chi-square(3.84), we have no convincing evidence to reject the null hypothesis. Thus the the data are consistent with the null hypothesis that there is no difference between the current account holders and savings account holders in the perceived satisfaction level.