Use the following quiz questions to check your understanding of density curves and normal distributions. Note that as soon as you have indicated your response, the question is scored and feedback is provided. As feedback is provided for each option, you may find it useful to try all of the responses (both correct and incorrect) to read the feedback, as a way to better understand the concept.
Guess the correlation
Guess the correlation
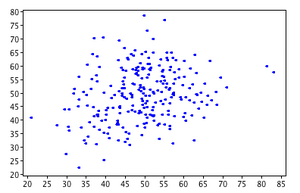
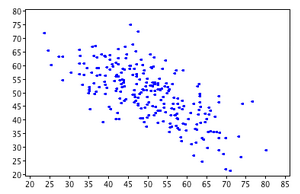
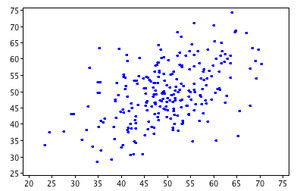
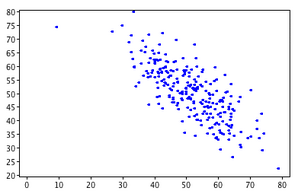
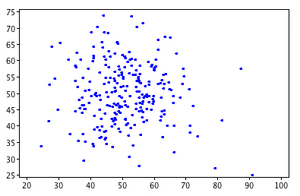
For each of the scatterplots shown, choose the most likely correlation value.[1]
- -.76
- That's not quite right. The direction of the relationship is positive. Try again.
- -.42
- That's not quite right. The direction of the relationship is positive. Try again.
- -.09
- That's not quite right. The direction of the relationship is clearly positive. Try again.
- .24
- That's correct. The direction of the relationship is positive and the linear relationship is weak (close to zero).
- .58
- That's not quite right. Although the direction of the relationship is positive, the linear relationship is not this strong. Try again.
- -.69
- That's correct. The direction of the relationship is negative and the linear relationship is moderate to strong.
- -.35
- That's not quite right. Although the direction of the relationship is negative, the linear relationship is stronger (closer to -1). Try again.
- -.02
- That's not quite right. Although the direction of the relationship is negative, the linear relationship is not near zero. Try again.
- .31
- That's not quite right. The direction of the relationship is negative. Try again.
- .65
- That's not quite right. The direction of the relationship is negative. Try again.
- -.53
- That's not quite right. The direction of the relationship is positive. Try again.
- -.20
- That's not quite right. The direction of the relationship is positive. Try again.
- .13
- That's not quite right. Although the direction of the relationship is positive, the linear relationship is stronger than this. Try again.
- .47
- That's correct. The direction of the relationship is positive and the linear relationship is moderate.
- .80
- That's not quite right. Although the direction of the relationship is positive, the linear relationship is not as strong as this. Try again.
- -.76
- That's correct. The direction of the relationship is negative and the linear relationship is strong (close to one).
- -.44
- That's not quite right. Although the direction of the relationship is negative, the linear relationship is stronger. Try again.
- .10
- That's not quite right. Look again at the direction and strength of the relationship. Try again.
- .58
- That's not quite right. Look again at the direction of the relationship. Try again.
- .97
- That's not quite right. Look again at the direction of the relationship. Try again.
- -.81
- That's not quite right. The direction of the relationship is not apparent, implying that the strength is non-existant (near zero). Try again.
- -.39
- That's not quite right. The direction of the relationship is not apparent, implying that the strength is non-existant (near zero). Try again.
- -.05
- That's correct. The direction of the relationship is not apparent and the strength is near zero. The fact that r is negative is irrelevant. If effect, there is no relationship between the variables portrayed in this scatterplot.
- .28
- That's not quite right. The direction of the relationship is not apparent, implying that the strength is non-existant (near zero). Try again.
- .61
- That's not quite right. The direction of the relationship is not apparent, implying that the strength is non-existant (near zero). Try again.
Understanding correlation
Properties of correlation
- The correlation between high school algebra and geometry final test scores was found to be +0.8. Which of the following statements is NOT true? (check all that apply.)[2]
- Most of the students who have above average scores in algebra also have above average scores in geometry.
- That's not quite right. This statement is true. A strong positive correlation does in fact indicate that higher values on one variable will tend to be higher also on the other variable. Try again.
- Most people who have above average scores in algebra will have below average scores in geometry.
- That's correct. This statement is incorrect. A strong positive correlation such as +.80 indicates that higher values on one variable will tend to be higher on the other variable.
- If a student increases his/her score in algebra (ie. with extra tutoring in algebra), then the student's geometry scores will always increase accordingly.
- That's correct. This statement is incorrect. A strong correlation of +.80 indicates that a positive relationship will hold generally, but not always.
- Most students who have below average scores in algebra also have below average scores in geometry.
- That's not quite right. This statement is true. A strong positive correlation does in fact indicate that lower values on one variable will tend to be lower also on the other variable. Try again.
- Which of the following is not a possible value for Pearson's correlation?[3]
- -1.5
- That's correct. A correlation can be any value between (and including) -1 and 1.
- -1
- That's not quite right. -1 is a valid value for a correlation, describing a perfect negative relationship. Try again.
- 0
- That's not quite right. 0 is a valid value for a correlation, describing a situation where the two variables have no relationship. Try again.
- .99
- That's not quite right. .99 is a valid value for a correlation, describing a near perfect positive relationship. Try again.
- Which is higher, the correlation between height and weight or the correlation between weight and height?[4]
- weight and height
- That's not quite right. Correlations are symmetric, which means order does not matter. Try again.
- They are about the same.
- That's not quite right. Correlations are symmetric, which means it doesn't matter which way the variables are assigned. Try again.
- They are exactly the same.
- That's correct. Correlations are the same regardless of which variable goes first, and does not require that variables be assigned as explanatory and response.
- height and weight
- That's not quite right. Correlations are symmetric, which means order does not matter. Try again.
- What is the effect on the correlation of adding 12 to every score on one variable? [5]
- The correlation may go up or down; it depends on the data.
- That's not quite right. Adding 12 to every score on one variable is a linear transformation. Consider what impact a linear transformation has on a correlation. Try again.
- The correlation will increase.
- That's not quite right. Adding 12 to every score on one variable is a linear transformation. Consider what impact a linear transformation has on a correlation. Try again.
- The correlation will not change.
- That's correct. The correlation is unaffected by a linear transformation, such as adding 12 to all of the scores in one variable.
}}
Notes
- ↑ Adapted from Guessing correlations demo at Online Statistics Education: An Interactive Multimedia Course of Study. Project Leader: David M. Lane, Rice University. Retrieved 17-18 September 2012.
- ↑ Question adapted from Ebook Problems GLM Corr, Problem 2 in Probability and Statistics EBook, from UCLA Statistics Online Computational Resource (SOCR), Retrieved 21 September 2012.
- ↑ Adapted from Properties of Pearson's r at Online Statistics Education: An Interactive Multimedia Course of Study. Project Leader: David M. Lane, Rice University. Retrieved 18 September 2012.
- ↑ Adapted from Properties of Pearson's r at Online Statistics Education: An Interactive Multimedia Course of Study. Project Leader: David M. Lane, Rice University. Retrieved 18 September 2012.
- ↑ Adapted from Computing Pearson's r at Online Statistics Education: An Interactive Multimedia Course of Study. Project Leader: David M. Lane, Rice University. Retrieved 18 September 2012.