Cautions about correlation and regression/Self-check assessment

Use the following quiz questions to check your understanding of simple linear regression. Note that as soon as you have indicated your response, the question is scored and feedback is provided. As feedback is provided for each option, you may find it useful to try all of the responses (both correct and incorrect) to read the feedback, as a way to better understand the concept.

Cautions

• Which of the following statements are true about residuals resulting from the fit of a least-squares regression line? (check all that apply)
  • They are the deviations of the observed values from the fitted line.
    • That's correct. A residual is the distance in the y-direction of the observed value and the fitted least-squares regression line.
  • They're closely related to the errors of prediction of the observation.
    • That's correct. We use the regression line to predict the most likely y value for a given x value; the difference between the actual value and the predicted value is the residual, which is also the error in prediction.
  • The formula to calculate each individual residual is: [math]residual = y - \hat{y}[/math].
    • That's correct. The residual, which is the deviation of the observed value from the fitted line in the y-direction, is calculated by subtracting the predicted y value from the observed y value.
  • Large residuals will lead to large influence on the regression model in all circumstances.
    • That's not quite right. A large residual will indicate an outlier in the regression, but whether or not this outlier has a large impact on the regression depends on the position of the other points which are closer to the line.
• 

  
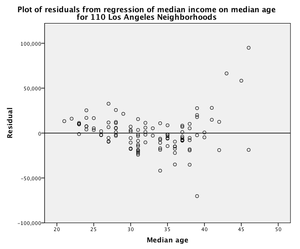
  Using data collected as part of the 2000 US Census, various statistics were obtained for 110 Los Angeles neighborhoods, including the median household income and median age of residents. The plot at right displays the residuals resulting from the linear regression of median income (response variable) on median age (explanatory variable). Without knowledge of the scatterplot of the two variables, what would you conclude about the form of the relationship between income and age and the appropriateness of using a least-squares regression line to describe it?
  • The scatter is reasonably random, suggesting a linear relationship. Least-squares regression is appropriate for describing this relationship.
    • That's not quite right. Although it is true that a linear relationship is required when using linear regression, the scatter of points in the residual plot does not suggest a linear relationship. Consider the pattern of points in the residual plot. Try again.
  • The scatter of points has an obvious pattern, suggesting the relationship may be curvilinear. Least-squares regression is not appropriate for describing this relationship.
    • That's correct. A linear relationship is required when using linear regression and the scatter of points in the residual plot displays a curved pattern suggesting the relationship may be curvilinear.
  • About half of the points are below the line with the other half above the line, suggesting a linear relationship. Least-squares regression is appropriate for describing this relationship.
    • That's not quite right. In order to suggest a linear relationship, which is required when using linear regression, the points must be randomly scattered above and below the line. Consider the pattern of points in the residual plot. Try again.
  • The residual plot is not useful for making a decision about the appropriate use of linear regression.
    • That's not quite right. For the collection of observations, the residual plot displays the distance from the observation to the fitted line in the y direction, providing an effective way to evaluate whether or not the relationship is linear (which is when the points are randomly scattered about the y=0 line). Try again.
• An educational psychologist finds a fairly strong correlation between the scores on a reading test and on a math test. The psychologist is curious about whether the relationship holds for both students who are above the median and for students who are below the median on the reading test. Therefore, the psychologist computes the correlation between reading and math for both these subgroups. How do you think these correlations will compare to the correlation with all students?
  • If there are no extreme scores the correlations should be about the same as the original correlation.
    • That's not quite right. Consider that the range of values for the reading and math test scores are now restricted in each of the sub-groups. Try again.
  • Since the sample sizes are smaller, the correlations should be higher in the lower and upper halfs than in the whole class.
    • That's not quite right. The size of a correlation is not related to the sample size. Rather, consider that the range of values for the reading and math test scores are now restricted in each of the sub-groups. Try again.
  • The correlations would be expected to be smaller in the lower and upper halves than in the whole class.
    • That's correct. The range of reading and math scores will be restricted when only the lower (or upper) half of the students are considered. This leads to a smaller correlation.
  • It depends on whether the students are better at math or better at reading.
    • That's not quite right. Consider that the range of values for the reading and math test scores are now restricted in each of the sub-groups. Try again.
  • The correlation would be higher in the upper half and lower in the lower half.
    • That's not quite right. Consider that the range of values for the reading and math test scores are now restricted in each of the sub-groups. Try again.

Cautions continued

• 

  
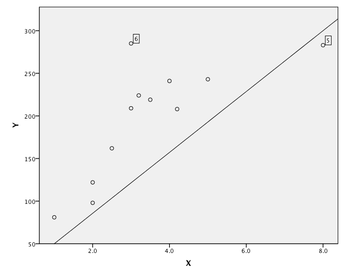
  The scatterplot at right displays the least squares regression line for a series of data points. Although point #6 is farthest away from the line, why would we consider point #5 to be the more influential? because
  • Point #5 is an outlier in the x direction (it has an x value much larger than all of the other data points). As such, it has a strong influence on the position of the linear regression line, and in this situation has influenced the placement of the regression line to be much closer to point #5 than it would have been if point #5 were not included in the dataset. Point #6 doesn't have nearly the level of influence due to the other points in its vicinity.
• If we were to calculate the residual values for points #5 and #6 given the linear regression line shown on the graph, point #5 would have a negative (positive/negative/zero) value and point #6 would have a positive (positive/negative/zero) value.
  • Hint: remember that the residual is the distance from the line in the y direction.
• If we removed point #5 from the dataset and reset the linear regression line, the slope of the line would likely increase (increase/decrease/remain the same/can't tell).