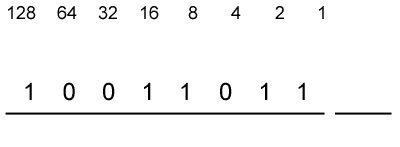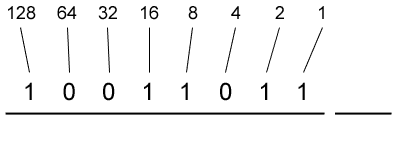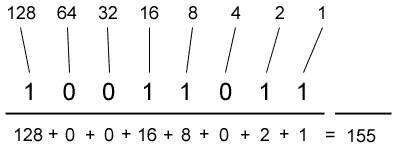Caribbean Secondary Education Certificate - Information Technology/Data Storage and Manipulation

Data Storage

Computer data storage, often called storage or memory, refers to computer components, devices, and recording media that retain digital data used for computing for some interval of time. Computer data storage provides one of the core functions of the modern computer, that of information retention. It is one of the fundamental components of all modern computers, and coupled with a central processing unit (CPU, a processor), implements the basic computer model used since the 1940s.

In contemporary usage, memory usually refers to a form of semiconductor storage known as random access memory (RAM) and sometimes other forms of fast but temporary storage. Similarly, storage today more commonly refers to mass storage - optical discs, forms of magnetic storage like hard disks, and other types slower than RAM, but of a more permanent nature. Historically, memory and storage were respectively called primary storage and secondary storage.

The contemporary distinctions are helpful, because they are also fundamental to the architecture of computers in general. As well, they reflect an important and significant technical difference between memory and mass storage devices, which has been blurred by the historical usage of the term storage.

Purpose of Storage

Many different forms of storage, based on various natural phenomena, have been invented. So far, no practical universal storage medium exists, and all forms of storage have some drawbacks. Therefore a computer system usually contains several kinds of storage, each with an individual purpose.

A digital computer represents data using the binary numeral system. Text, numbers, pictures, audio, and nearly any other form of information can be converted into a string of bits, or binary digits, each of which has a value of 1 or 0. The most common unit of storage is the byte, equal to 8 bits. A piece of information can be handled by any computer whose storage space is large enough to accommodate the binary representation of the piece of information, or simply data. For example, using eight million bits, or about one megabyte, a typical computer could store a small novel.

Traditionally the most important part of every computer is the central processing unit (CPU, or simply a processor), because it actually operates on data, performs any calculations, and controls all the other components.

Without a significant amount of memory, a computer would merely be able to perform fixed operations and immediately output the result. It would have to be reconfigured to change its behavior. This is acceptable for devices such as desk calculators or simple digital signal processors. Von Neumann machines differ in that they have a memory in which they store their operating instructions and data. Such computers are more versatile in that they do not need to have their hardware reconfigured for each new program, but can simply be reprogrammed with new in-memory instructions; they also tend to be simpler to design, in that a relatively simple processor may keep state between successive computations to build up complex procedural results. Most modern computers are von Neumann machines.

In practice, almost all computers use a variety of memory types, organized in a storage hierarchy around the CPU, as a tradeoff between performance and cost. Generally, the lower a storage is in the hierarchy, the lesser its bandwidth and the greater its access latency is from the CPU. This traditional division of storage to primary, secondary, tertiary and off-line storage is also guided by cost per bit.

Tertiary Storage

Tertiary storage or tertiary memory, provides a third level of storage. Typically it involves a robotic mechanism which will mount (insert) and dismount removable mass storage media into a storage device according to the system's demands; this data is often copied to secondary storage before use. It is primarily used for archival of rarely accessed information since it is much slower than secondary storage (e.g. 5-60 seconds vs. 1-10 milliseconds). This is primarily useful for extraordinarily large data stores, accessed without human operators. Typical examples include tape libraries and optical jukeboxes.

When a computer needs to read information from the tertiary storage, it will first consult a catalog database to determine which tape or disc contains the information. Next, the computer will instruct a robotic arm to fetch the medium and place it in a drive. When the computer has finished reading the information, the robotic arm will return the medium to its place in the library.

Offline Storage

Off-line storage, also known as disconnected storage, is a computer data storage on a medium or a device that is not under the control of a processing unit. The medium is recorded, usually in a secondary or tertiary storage device, and then physically removed or disconnected. It must be inserted or connected by a human operator before a computer can access it again. Unlike tertiary storage, it cannot be accessed without human interaction.

Off-line storage is used to transfer information, since the detached medium can be easily physically transported. Additionally in case a disaster, for example a fire, destroys the original data, a medium in a remote location will be probably unaffected, enabling disaster recovery. Off-line storage increases a general information security, since it is physically inaccessible from a computer, and data confidentiality or integrity cannot be affected by computer-based attack techniques. Also, if the information stored for archival purposes is accessed seldom or never, off-line storage is less expensive than tertiary storage.

In modern personal computers, most secondary and tertiary storage media are also used for off-line storage. Optical discs and flash memory devices are most popular, and to much lesser extent removable hard disk drives. In enterprise uses, magnetic tape is predominant. Older examples are floppy disks, Zip disks, or punched cards.

Characteristics of Storage

Storage technologies at all levels of the storage hierarchy can be differentiated by evaluating certain core characteristics as well as measuring characteristics specific to a particular implementation. These core characteristics are volatility, mutability, accessibility, and addressibility. For any particular implementation of any storage technology, the characteristics worth measuring are capacity and performance.

Volatility

• Non-volatile memory

Will retain the stored information even if it is not constantly supplied with electric power. It is suitable for long-term storage of information. Nowadays used for most of secondary, tertiary, and off-line storage. In 1950s and 1960s, it was also used for primary storage, in the form of magnetic core memory.

• Volatile memory

Requires constant power to maintain the stored information. The fastest memory technologies of today are volatile ones (not a universal rule). Since primary storage is required to be very fast, it predominantly uses volatile memory.

Differentiation

• Dynamic memory

A form of volatile memory which also requires the stored information to be periodically re-read and re-written, or refreshed, otherwise it would vanish.

• Static memory

A form of volatile memory similar to DRAM with the exception that it does not refresh on occasion.

Mutability

• Read/write storage or mutable storage

Allows information to be overwritten at any time. A computer without some amount of read/write storage for primary storage purposes would be useless for many tasks. Modern computers typically use read/write storage also for secondary storage.

• Read only storage

Retains the information stored at the time of manufacture, and write once storage (WORM) allows the information to be written only once at some point after manufacture. These are called immutable storage. Immutable storage is used for tertiary and off-line storage. Examples include * CD-ROM and CD-R

Slow write, fast read storage

Read/write storage which allows information to be overwritten multiple times, but with the write operation being much slower than the read operation. Examples include CD-RW.

Accessibility

• Random access

Any location in storage can be accessed at any moment in approximately the same amount of time. Such characteristic is well suited for primary and secondary storage.

• Sequential access

The accessing of pieces of information will be in a serial order, one after the other; therefore the time to access a particular piece of information depends upon which piece of information was last accessed. Such characteristic is typical of off-line storage.

Addressability

• Location-addressable

Each individually accessible unit of information in storage is selected with its numerical memory address. In modern computers, location-addressable storage usually limits to primary storage, accessed internally by computer programs, since location-addressability is very efficient, but burdensome for humans.

• File addressable

Information is divided into files of variable length, and a particular file is selected with human-readable directory and file names. The underlying device is still location-addressable, but the operating system of a computer provides the file system abstraction to make the operation more understandable. In modern computers, secondary, tertiary and off-line storage use file systems.

• Content-addressable

Each individually accessible unit of information is selected with a hash value, or a short identifier with a number pertaining to the memory address the information is stored on. Content-addressable storage can be implemented using software (computer program) or hardware (computer device), with hardware being faster but more expensive option.

Capacity

• Raw capacity

The total amount of stored information that a storage device or medium can hold. It is expressed as a quantity of bits or bytes (e.g. 10.4 megabytes).

• Density

The compactness of stored information. It is the storage capacity of a medium divided with a unit of length, area or volume (e.g. 1.2 megabytes per square inch).

Performance

• Latency

The time it takes to access a particular location in storage. The relevant unit of measurement is typically nanosecond for primary storage, millisecond for secondary storage, and second for tertiary storage. It may make sense to separate read latency and write latency, and in case of sequential access storage, minimum, maximum and average latency.

• Throughput

The rate at which information can be read from or written to the storage. In computer data storage, throughput is usually expressed in terms of megabytes per second or MB/s, though bit rate may also be used. As with latency, read rate and write rate may need to be differentiated. Also accessing media sequentially, as opposed to randomly, typically yields maximum throughput.

Reference

Computer Storage

Data Manipulation

=== CONVERTING FROM DECIMAL TO BINARY ===

The decimal (base ten) numeral system has ten possible values (0,1,2,3,4,5,6,7,8, or 9) for each place-value. In contrast, the binary (base two) numeral system has two possible values, often represented as 0 or 1, for each place-value.

To avoid confusion while using different numeral systems, the base of each individual number may be specified by writing it as a subscript of the number. For example, the decimal number 156 may be written as 15610 and read as "one hundred fifty-six, base ten". The binary number 10011100 may be specified as "base two" by writing it as 10011100.

Since the binary system is the internal language of electronic computers, serious computer programmers should understand how to convert from decimal to binary. Although, converting in the opposite direction, from binary to decimal, is often easier to learn first.

==== STEPS ====

Comparison with descending powers of two and subtraction

1. List the powers of two in a "base 2 table" from right to left. Start at 20, evaluating it as "1". Increment the exponent by one for each power. The list, to ten elements, would look like this: 512, 256, 128, 64, 32, 16, 8, 4, 2, 1
2. For this example, let's convert the decimal number 15610 to binary. What is the greatest power of two that will fit into 156? Since 128 fits, write a 1 for the leftmost binary digit, and subtract 128 from your decimal number, 156. You now have 28.
3. Move to the next lower power of two. Can 64 fit into 28? No, so write a 0 for the next binary digit to the right.
4. Can 32 fit into 28? No, so write a 0.
5. Can 16 fit into 28? Yes, so write a 1, and subtract 16 from 28. You now have 12.
6. Can 8 fit into 12? Yes, so write a 1, and subtract 8 from 12. You now have 4.
7. Can 4 (power of two) fit into 4 (working decimal)? Yes, so write a 1, and subtract 4 from 4. You have 0.
8. Can 2 fit into 0? No, so write a 0.
9. Can 1 fit into 0? No, so write a 0.
10. Since there are no more powers of two in the list, you are done. You should have 10011100. This is the binary equivalent of the decimal number 156. Or, written with base subscripts: 15610 = 100111002

• Repetition of this method will result in memorization of the powers of two, which will allow you to skip step 1.

Short division by two with remainder This method is much easier to understand when visualized on paper. It relies only on division by two.

For this example, let's convert the decimal number 15610 to binary. Write the decimal number as the dividend inside an upside-down "long division" symbol. Write the base of the destination system (in our case, "2" for binary) as the divisor outside the curve of the division symbol. 2)156

Write the integer answer (quotient) under the long division symbol, and write the reminader (0 or 1) to the right of the dividend. 2)156 0

  78

Continue downwards, dividing each new quotient by two and writing the remainders to the right of each dividend. Stop when the quotient is 1. 2)156 0

2)78   0
2)39   1
2)19   1
 2)9   1
 2)4   0
 2)2   0
   1

Starting with the bottom 1, read the sequence of 1's and 0's upwards to the top. You should have 10011100. This is the binary equivalent of the decimal number 156. Or, written with base subscripts: 156 = 10011100

Reference

How to convert from decimal to binary

CONVERTING FROM BINARY TO DECIMAL

The binary (base two) numeral system has two possible values, often represented as 0 or 1, for each place-value. In contrast, the decimal (base ten) numeral system has ten possible values (0,1,2,3,4,5,6,7,8, or 9) for each place-value.

To avoid confusion while using different numeral systems, the base of each individual number may be specified by writing it as a subscript of the number. For example, the binary number 10011100 may be specified as "base two" by writing it as 10011100. The decimal number 156 may be written as 156 and read as "one hundred fifty-six, base ten".

Since the binary system is the internal language of electronic computers, serious computer programmers should understand how to convert from binary to decimal. Converting in the opposite direction, from decimal to binary, is often more difficult to learn first.

Note: This is ONLY for counting and does not talk about ASCII translations.

STEPS

TABLE METHOD

1. For this example, let's convert the binary number 100110112 to decimal. List the powers of two from right to left. Start at 2, evaluating it as "1". Increment the exponent by one for each power. Stop when the amount of elements in the list is equal to the amount of digits in the binary number. The example number, 10011011, has eight digits, so the list, to eight elements, would look like this: 128, 64, 32, 16, 8, 4, 2, 1
2. Write the binary number below the list.

1. Draw lines, starting from the right, connecting each consecutive digit of the binary number to the power of two that is next in the list above it. Begin by drawing a line from the first digit of the binary number to the first power of two in the list above it. Then, draw a line from the second digit of the binary number to the second power of two in the list. Continue connecting each digit with its corresponding power of two.

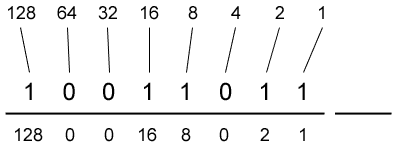
1. Move through each digit of the binary number. If the digit is a 1, write its corresponding power of two below the line, under the digit. If the digit is a 0, write a 0 below the line, under the digit.

1. Add the numbers written below the line. The sum should be 155. This is the decimal equivalent of the binary number 10011011. Or, written with base subscripts: 100110112 = 15510

1. Repetition of this method will result in memorization of the powers of two, which will allow you to skip step 1.

DOUBLING METHOD

Starting from zero, and working from left to right, double your number and add the next digit of the base two representation. For example to convert 1011001, we take the following steps.

1|011001 0*2+1 = 1 10|11001 1*2+0 = 2 101|1001 2*2+1 = 5 1011|001 5*2+1 = 11 10110|01 11*2+0 = 22 101100|1 22*2+0 = 44 1011001 44*2+1 = 89

Reference

Converting from Binary to Decimal