AfroPhysics/Project Planning/Uganda/Good Ideas3 (section)/Astro13/Interplanetary Space

Hubarbeit in Gravitational field

A missile to a heavenly body removed far from the earth to send is above all an energetic question. How can the need of fuel be minimized?

We go out first of the work to raise a spacecraft in the gravitational field of the earth from the surface. Unfortunately the comfortable formula is valid

WH = m g h

only in direct proximity of the surface, because it contains the local factor g, which depends on the place. We know already that far removes outside the gravitation after the Newton's gravitation law:
F_grav = [math]G \frac{M m}{r^2}[/math]

The agreement of both relations at the earth's surface opens an elegant possibility of computing the mass of the earth (see task of A….)!

How do we compute thus the Hubarbeit for large heights?

Report: An integration of the gravitation strength over the vertical lift results in the expression

[math]W_H = G M m ( \frac{1}{r_1} - \frac{1}{r_2} )[/math]

whereby g 1 is at the beginning of and r2 the final radius. M is the mass of the earth, m the mass of the elevated body.

We recognize that for r2 > g 1 becomes positive the expression for WH, which means that work must be spent.

If the spaceship is lifted of the earth's surface into the infinite, is called the r2 becomes infinitely, and thereby

[math]W_H = G M  \frac{m}{R}[/math]

whereby R is the Erdradius.

A12. Mass of the earth, mass of the sun

a) Compute the mass of the earth with the help of the local factor g and the Newton's gravitation law, evaluated at the earth's surface!
b) Compute the mass of the sun from the rotating data of the earth, with the help of the numerical value for the astronomical unit!

Escape velocity

In its famous novel “from the earth to the moon” of 1865 Jules Verne describes, how a manned space cap with a cannon is shot to the moon. We call the speed, with which the projectile would have to leave the cannon pipe, the escape velocity. It is more exact the smallest speed, in order to leave the earth on Nimmerwiedersehen.

We determine it from the energy beginning

Ekin = Epot

Receive and

 [math]v_F = \sqrt{\frac{2 G M}{R}}[/math]

A13. Impact

• a) Compute the escape velocity of the ground connection and lunar surface!
• b) Set up an assumption, why around the earth an atmosphere can exist, not however around the moon! Note: Think of the kinetic gas theory!
• c) How largely is the impact speed meteorites at least on earth and/or the moon? Note: It may be assumed the meteorite from the infinite one without substantial deceleration in the atmosphere falls down.

== High Course Man ==

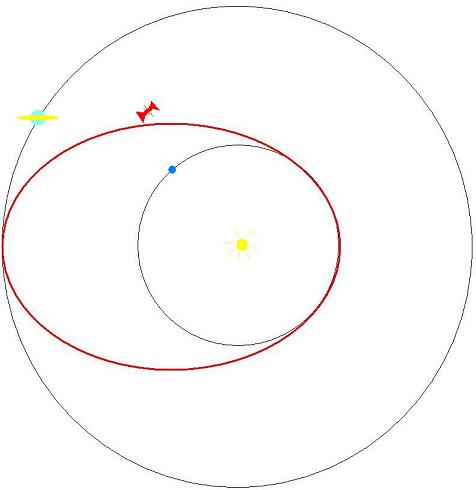
If a space probe departed a good piece from the earth, it circles more or less on the orbit of the earth around the sun. If we want to reach now an outside planet, for instance the Saturn, the spacecraft must be accelerated, so that it reaches the Perihelgeschwindigkeit of an ellipse, whose aphelion lies on the course of the Saturn. Note that the sun stands in the focus of this ellipse!

Such a course is energetic at the most favorable one, even if in space practice spiral courses are often preferred. We call it the high man course from the earth to the Saturn.

Regard to it also in the Internet the simulation of a flight to Jupiter.

If we want to compute the airspeed at any place of the course, then we know the formula use, which find you also in the collection of formulae. (Without proof.)

[math]v = \sqrt{G M ( \frac{2}{r} - \frac{1}{a} ) }[/math]

r is thereby the momentary distance of the sun, and The large shaft section of the ellipse.

In particular thereby the perihel and aphelion speed are calculable.