Kepler's Laws

|

First Law

The planets (and nearly all other objects in the solar system) move in paths, which have the form of ellipses. The sun stands in one of the two focuses.Italic text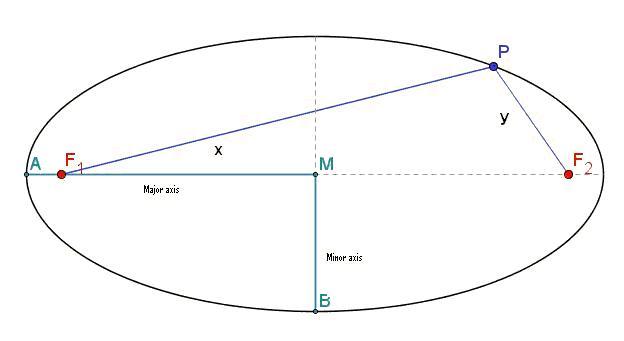 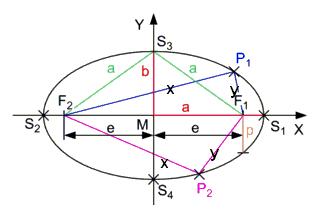The defining characteristic of an ellipse is

x+y=contant

Note: Thus a circle is a special case of an ellipse. The eccentricity of an ellipse

After Phythagoras is valid

e2 + b2 = d2

In addition, it is valid

A = D (because of x + y = (A + e) + (A e))

and thus

e2 + b2 = a2 thus

e =  \ {a^2 sqrt - b^2}  called the accentricity
\ varepsilon = \ frac {e} {A}

A1. Aphelion and Perihel

Show that the average value from the largest and the smallest distance of a planet of the sun (aphelion, Perihel) is equal to the large shaft section of the course.

A2. Comet Path

The comet Encke has a distance of 0,339 and/or 4,094 astronomical units (AE) of the sun in the Perihel and aphelion of its course.

• a) Compute the large and the small shaft section as well as the numeric eccentricity of the course!
• b) Manufacture a design true to scale of the ellipse path! (1AE corresponds to 2 cm)

A3. Mars Path

Johannes Kepler counted 8 years, in order to find out that Mars describes not a circular path, but an ellipse around the sun. Its results were astonishing exactly, although the numeric eccentricity of the course only \ varepsilon = 0,093 amounts to.

• a) Compute the small shaft section, if the large shaft section A = 1.524 amounts to AE, and the difference of the shaft sections in %!
• b) Manufacture a design true to scale of the coordinate system!
• c) Which largest and/or smallest distance of the sun can reach Mars?