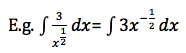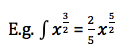Level 3 Calculus - Integration

Integrating polynomials and evaluating the constant of integration.

Delta textbook chapter 16, pages 158 – 162, exercises 16.1 – 16.3

Symbols:
c is a constant of integration.
^ means to the power of
/ means divided by

Rule of Integration

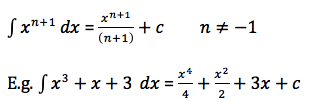
If you can expand the function first, do.

You can also bring variables and their powers up from the bottom of a fraction by making the power negative.

When something is divided by a fraction, flip the fraction upside-down and multiply by it instead.

Simplify as much as you can in any situation.

When in doubt, check your answer by differentiating it to see whether the result is the function you are trying to integrate.

To find the value of c - (evaluating the constant of integration) - you must first be given values for x and y. If they are given, all you need to do is substitute them into your equation to find c!

If you ever have two constants and two values for both x and y, solve a simultaneous equation to find both constants.

Integrating e^(x) and 1/(x)

Delta textbook chapter 16, pages 162 – 164, exercises 16.4 – 16.5

‘Integrating e is easy!’

Similar to differentiation, leave e^(n) alone. The only difference is that instead of multiplying by the differentiation of n, we divide by it instead. Don’t forget the constant!

For 1/(x) the rule is (for all values of x):

Often a pre-multiplier has to be added at the front of the answer to ‘balance’ the effect of the chain rule.

The numerator stays the same, the denominator becomes whatever value is in front of the variable.

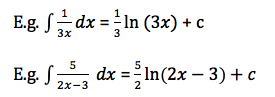
Always simplify before you attempt to integrate harder questions.

When in doubt, check your answer by differentiating it to see whether the result is the function you are trying to integrate.

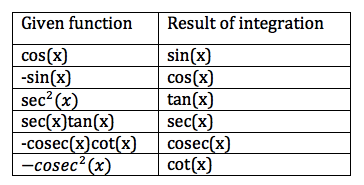
Integrating Trig Functions

If you are given a reverse function, e.g. –cos(x) instead of cos(x), the result is the reverse of the result, e.g. –sin(x) instead of sin(x).

Integrating Trig Products

Delta textbook chapter 17, page 168, exercise 17.2

To integrate a trig product first turn it into a sum using the formula on your formula sheet.

(This can be found on the nzqa website here as the formulae resource for any calculus exam: http://www.nzqa.govt.nz/ncea/assessment/search.do?query=calculus&view=exams&level=03)

If you do not have the required ‘2’ at the front of your product you must substitute a ‘2’ for now but at the end multiply your answer by the original amount you had in relation to the ‘2’.

e.g. If you have sinAcosB when the formula is 2sinAcosB, turn it into a sum following the formula like you have a 2 in front, (sin(A+B) + sin(A-B)), and integrate the parts separately, (-cos(A+B) – cos(A-B)). Then, because you started with half the formula you multiply by ½ and your final answer becomes -0.5cos(A+B) – 0.5cos(A-B).

If you have 5sinAcosB, you will multiply by 5/2 at the end, and so on.