User:Lisa

KNUSPER KNUSPER KNÄUSCHEN

x(t)= [math]x_0[/math] + v*t

[math]\Delta x[/math] = v* [math]\Delta t[/math]

v= [math]\frac {x}{t} [/math]

v= [math]\frac {x_1-x_0}{\Delta t}[/math]

[math]x_1[/math](t)= [math]x_2[/math](t)

[math]x_1+v_1*t = x_2+v_2*t[/math]

[math]x_1-x_2 = (v_2-v_1)*t[/math]

[math]t = \frac {x_1-x_2}{v_2-v_1}[/math] = [math]\frac {173m-25m}{28km/h-11km/h}[/math]

Unser Poster

Mei, wie schee !!!

Unser Kambotscha Projekt

Da können die Kinder richtig viel lernen !

Das könnt ihr niemals toppen ;)

Kein Wunder das wir die einzige 1 bekommen haben :P

Schön schön schön ...

Verbesserung der 1. Extemporale

a)

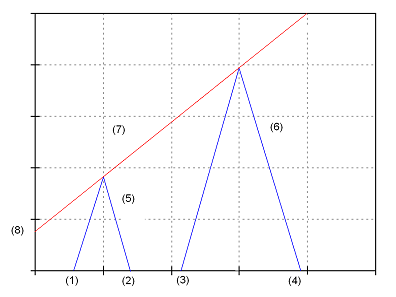Rechtswert: Zeit t , Hochwert: Ortskoordinate x

b) x₁ = v * [math]\frac {\Delta t} {2} [/math]

[math]\Delta t[/math] = t₂ - t₁

= 0.30s

sandbox

Exercise 2.7: From zero to hundred

The test run of a new motorbike gave a rate growth from 0 to 100 km/h in 3,87 s. WORK OUT THE middle speedup and the way it put back at this speedup and this time!

Solution

Exercise 2.8: Train ride

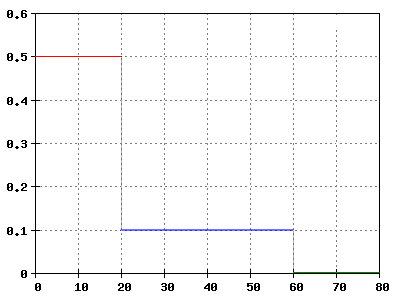
Easting: time t in s

Northing: speedup a in m/s^2

A train starts moving. The diagram shows the dependence of its middle speedup of time.

a) Work out the rate growth from the train after 20 s, 60 s and 80 s and draw the t-v-diagram b) Work out with the help of the t-v-diagram the way it put back for the same point of time and draw a t-x-diagram

Solution

Exercise 2.9: Bullet

The ball of a gun should constant speed up in its barrel.

a) After what time the ball leaves the barrel b) How big is the speedup if the 18 cm long barrel will be left with 760 m/s.

Solution

Exercice 2.10: Cavalier’s start?

At the start of a car you grab the following measured values:

Zeit t in s	Ort x in m
0	0
1	0,5
2	2
3	4,5
4	8
4,2	8,8
5	12
6	16
7	20

a) With which way-time-functions the movements leave themselves in time sections to 0 < t < 4 s and 4 s < t < 7 s describe? b) Intend acceleration and the momentary speed for each point of the chart! Draw the (t) diagram! Determine from it with the help of the surface the place x(6,5 s) to t = 6.5 s!

Solution

Aufgabe 3.7: Gehalten !

a)

Lösung: v² = 2ax

--> a = v²/2x

a = 3836 m/s²

F = m * a

F = 0,50 kg * 3836 m/s²

F = 1918 N

Aufgabe 4.3: Spann die Feder

geg.: F = 50 N s = 80 cm = 0,8 m

a) ges.: W_sp

Lösung: F = D*s => D = F/s = 50 N/0,8 m = 62,5 N/m

W_sp = 1/2 D*s = 1/2 * 62,5 N/m * (0,8)² = 20 J

Aufgabe 4.9: Strafstoß

Lösung:

geg.:
m = 450 g = 0,45 kg
t = 0,030 s
F = 400 N

a) ges.: p
p = F*t
p = 400 N * 0,030 s = 12 Ns

b) ges.: v
p = m*v
v = p/m
v = 12 Ns / 0,45 kg = 26,67 m/s

c) ges.: a
a = v/t
a = 26,67 m/s / 0,030 s = 889 m/s²

d) ges.: v
v = a*t
v = 889 m/s² * 0,030 s = 26,67 m/s

Aufgabe 5.6: Schleuderball mit Tücken

geg.:
m = 0,80 kg
r = 50 cm = 0,50 m
v = 3,4 m/s

a)
am höchsten Punkt:
F_z = m *w² * r
= m * (v/r)² * r
= m * v²/r
= 0,80 * (3,4)²/0,50
= 18,5 N

F_G = m * g = 0,80 * 9,81 = 7,8 N
F_Schnur = F_Z - F_G
F_Schnur = 18,5 N - 7,8 N
F_Schnur = 10,7 N

am tiefsten Punkt:
F_Schnur = 18,5 N + 7,8 N = 26,3 N

Aufgabe 5.9: Nervenkitzel

geg.: r = 20 m
v = 40 km/h = 11,11 m/s
m = 250 kg

ges.: Neigungswinkel a

tan a = F_ZF/F_G
m*w²*r/m*g = (v/r)²*r/g = v²/r*g =
(11,11 m/s)²/20 m * 9,81 m/s² = 0,63
=> Neigungswinkel a = 32,2 °

Aufgabe 5.13 : Ausflug auf den Reiterhof

Anni, Valli & Lissi machen einen Ausflug auf den Reiterhof.
Nachdem sie ihr Lieblingspferdchen Detlef D! Soost gestriegelt und gezäumt haben beginnen sie mit ihren voltigier Übungen. Als erstes lassen sie ihn an einer Leine von 8 m im Kreis laufen. Für eine Runde braucht er in Galopp 45 s.

a) Berechnen Sie die Winkelgeschwindigkeit sowie die normale Geschwindigkeit
die D! für eine Runde braucht.

Plötzlich kommt der Star Detlef D! Soost Vallis, Annis & Lissis Angebeteter um die Ecke. Als Detlef auf sein Namensfetterpferd steigt können die 3 es kaum glauben.