Type I and type II errors

From WikiEducator
Jump to: navigation, search

A statistical hypothesis test is a method of making decisions using data. The results of a hypothesis test consist of four possible outcomes depending on the actual truth (or falseness) of the null hypothesis H0 and the decision to reject or not. In two of the four outcomes our decision corresponds with the actual situation, while for the other two outcomes our decision is in error, either a type I or a type II error.

The logic behind decision errors

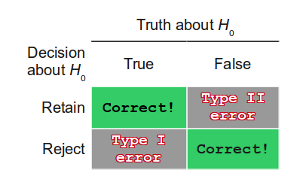
Statistical inference as a decision
Given the results of a hypothesis test, researchers may conclude one of two possibilities (the two rows in the table at right).
  1. The observed pattern of data is likely due to chance: we fail to reject H0 and conclude the results are not statistically significant--a negative result. (Row 1)
  2. The observed pattern of data is likely not due to chance: we reject H0 and conclude the results are statistically significant--a positive result. (Row 2)

But, no matter how well the study is designed and performed, either conclusion may be wrong.

In fact, we have two possibilities for the truth about the population we are studying (labeled "Truth about H0, the two columns in the table). Note that this truth is unknown to us before and after we perform the statistical test. When we consider the researcher's two possible conclusions, against the two possibilities for the true state of the population, we arrive at the four possible outcomes for a hypothesis test.

Let's go back to think about the researcher's two possible conclusions. When the researcher makes a mistake about the second conclusion, reject H0 when in fact it is true, s/he is making a type I error. When the researcher makes a mistake about the first conclusion, fail to reject H0 when in fact it is false, s/he is making a type II error.

Note that a type I error is only possible in a study whose results are statistically significant (a positive conclusion), and a type II error is possible only in a study which fails to find significance (a negative conclusion).

The probability of error

By common convention, if the probability value is below 0.05 (or 0.01, if a more stringent criterion is desired) then the null hypothesis is rejected. This threshold, or significance level, for rejecting the null hypothesis is called the α level or simply α. Note that although it is tempting to use the significance level as part of a decision rule for making a reject or do-not-reject decision, it is better to interpret the probability value as an indication of the weight of evidence against the null hypothesis. Rejecting the null hypothesis is not an all-or-nothing decision.

The Type I error rate is affected by the α level: the lower the α level the lower the Type I error rate. It might seem that α is the probability of a Type I error. However, this is not correct. Instead, α is the probability of a Type I error given that the null hypothesis is true. If the null hypothesis is false, then it is impossible to make a Type I error.

The second type of error that can be made in significance testing is failing to reject a false null hypothesis. This kind of error is called a Type II error. Unlike a Type I error, a Type II error is not really an error. When a statistical test is not significant, it means that the data do not provide strong evidence that the null hypothesis is false. Lack of significance does not support the conclusion that the null hypothesis is true. Therefore, a researcher would not make the mistake of incorrectly concluding that the null hypothesis is true when a statistical test was not significant. Instead, the researcher would consider the test inconclusive. Contrast this with a Type I error in which the researcher erroneously concludes that the null hypothesis is false when, in fact, it is true.

A Type II error can only occur if the null hypothesis is false. If the null hypothesis is false, then the probability of a Type II error is called β. The probability of correctly rejecting a false null hypothesis equals 1- β and is called power.

An example

Suppose the null hypothesis, Ho, is: Frank's rock climbing equipment is safe.

Type I error: Frank concludes that his rock climbing equipment may not be safe when, in fact, it really is safe. Type II error: Frank concludes that his rock climbing equipment is safe when, in fact, it is not safe.

α = probability that Frank thinks his rock climbing equipment may not be safe when, in fact, it really is. β = probability that Frank thinks his rock climbing equipment is safe when, in fact, it is not.

Notice that, in this case, the error with the greater consequence is the Type II error. (If Frank thinks his rock climbing equipment is safe, he will go ahead and use it.)

Self-check assessment

Type I and type II errors self-check assessment

Acknowledgements

Portions of this page were adapted from

Retrieved from "https://wikieducator.org/index.php?title=Type_I_and_type_II_errors&oldid=701139"