Consequences of the Second Law
| Thermodynamics | |
|---|---|
| Introduction | What is this thing called Thermodynamics??? | Definitions | Thermal Equilibrium and Zeroth Law | Limitations |
| First Law | Work, Heat, Energy, and the First Law | Work, Heat, Energy, and the First Law (simplied) | Derivatives | Derivatives Exercise | Reversibility, Enthalpy, and Heat Capacity |
| Second Law | Things to Think About | Observations and Second Law of Thermodynamics | Alternative Approach - the Clausis Inequality | Consequences of the Second Law | Consequences of the Second Law (simplified) | Carnot Principle - motivation and examples | Equivalence of Second Law Statements* |
| Third Law | Third Law of Thermodynamics | Consequences of Third Law* |
| Development of Thermodynamics | The Thermodynamic Network | Network Exercise | Equations of State (EOS) | EOS Example, Reading Tables, and Numerical Analysis | EOS Exercises | Thermochemistry |
* Optional Section | |
Contents
Heat Engines
A Heat Engine is a cyclic process which converts heat into energy. By cyclic we mean that the process begins and ends in the same state. The cycle can either been within a single device or in devices linked together. The two most common types of heat engines are the internal combustion engine in a car and the electric power plant
Figure 1 shows a typical heat engine used for power generation. A fluid known as the working fluid is used, most commonly water. Water is heated in the boiler to create steam. The boiler can be heated by coal, oil, natural gas, nuclear, solar[1], biomass, or geothermal). The steam is then used to drive a turbine. The turbine consists of blade attached to a shaft. The shaft is connected to a dynamo to generate electricity. The steam leaving the turbine is then condensed back to water (releasing heat) and then pumped back to the boiler.
The second law of thermodynamics says No system can be developed which completely converts heat to work. So the second law should give some insight into heat engines. In doing so we will also learn some things about energy in general.
Since all of the heat entering a heat engine is not converted to work there must be some leftover heat. This is called waste heat.
Efficiency
- Efficiency, η
- The ratio of the net work to the heat input.
[math]\eta=\frac{-W_{net}}{Q_{in}}[/math]
Therefore, efficiency is the fraction of heat which is converted to work.
One confusion often for students is that in the above formula the work is the net work, that is, the work output minus the work input. Whereas the heat is only the heat in.
Carnot Cycle
The Carnot[2] cycle is a theoretical heat engine composed of four steps:
- Reversible, isothermal expansion of a gas
- Reversible, adiabatic expansion - cooling the gas
- Reversible, isothermal compression
- Reversible, adiabatic compression, returning the gas to its original state
Carnot Efficiency
The efficiency of a Carnot cycle is
[math]\eta_{Carnot}=\frac{T_H-T_C}{T_H}[/math]
where TH is the temperature of the heat source and TC is the temperature of the heat released. Remember in thermodynamics all temperatures are absolute.
Interesting about this is that the efficiency is based on only the temperatures, not on the internal workings of the cycle.
Carnot Principle
So why do we study the Carnot cycle? The answer lies in the Carnot Principle:
The maximum efficiency of a real cycle is the efficiency of a Carnot cycle operating over the same temperatures
The Carnot efficiency is often used a limiting efficiency and to compare with real efficiencies.
Refrigerators and Heat Pumps
A refrigerator is a device which removes heat from a colder region to a warm region. Note that an air conditioner is really a type of refrigerator. Figure 2 shows a diagram of a refrigerator.
In a refrigerator the working fluid is known as a refrigerant. The refrigerant enters the evaporator as a liquid. It evaporates, absorbing heat from the room or the inside of the refrigerator. The refrigerant is then compressed and sent to the condenser. In the condenser the refrigerant condenses, releasing heat to the outside. Finally, the refrigerant enters an expansion valve, which is a partially open valve.
The second law can be restated as the following (known as the Clausis statement):
Heat cannot be moved from a colder region to a hotter region without doing work.
A heat pump is the same as refrigerator, except that its purpose is to heat a region rather than cool it.
COP
For a refrigerator or heat pump, we are interested in the minimum amount of work. So efficiency is not the best measure. Instead of efficiency we use the Coefficient of Performance (COP). For a refrigerator the COP is:
[math]COP_R=\frac{Q_{in}}{W_{net}}[/math]
For a heat pump
The difference between these is what we are interested in. For a refrigerator we are interested in the amount of heat we remove, whereas for a heat pump we are interested in the amount of heat we get.
Note that COP is always greater than one.
The maximum COP is the Carnot COP:
[math]COP_{R,Carnot}=\frac{T_C}{T_H-T_C}[/math]
[math]COP_{HP,Carnot}=\frac{T_H}{T_H-T_C}[/math]
Efficiencies
Power Plants
A typical power plant has a Carnot efficiency of about 45%.[3]
Real efficiencies are at most 75% of the Carnot efficiency. Therefore, the overall efficiency is about 30%.
In other words, only about one-third of the energy from burning the fuel is converted to work. The rest is expelled as heat.
Figure 2 is an electricity flow chart for the United Kingdom in the year 2007. It shows input resources and output uses of electricity, where the width of the bars are proportional to the amount of energy. We can see the effects of efficiency by looking at the conversion losses (the gray bar), which dwarfs the other outputs.
Other Efficiencies
Let us at the efficiencies of some other processes:
- Fuel Cell 60%
- Human Body 25%
- Florescent Light 15%
- Car Engine 10%
- Incandescent Light 5%
The human body is only 25% efficient, which is why a room full of people is warmer than a empty room - all those people are giving off heat.
G. Tyler Miller calls an incandescent light bulb a "heat bulb" because it produces much more heat than light. The difference in efficiencies between types of light bulbs is why compact fluorescent lights are recommended over incandescent lights.
Consequences
- The concept of efficiency is the basis behind the all the concerns with energy issues. But note that the term energy crisis is a misnomer, energy is conserved. Rather it is a crisis in the quality of energy.
- There has been renewed interest in "renewable energies" - technology such as wind energy. Most of these (but not all) belong to what are called direct energy conversions. These do not convert heat to work (and therefore do not run in a cycle) and so are not limited by the Carnot efficiency.
- One practice that can be used with a thermal power plant is cogeneration, which is where the excess heat expelled is used to heat either an industrial process or buildings.
- The heat expelled from a cycle must go somewhere. It is usually captured by water which is then released into a lake or the sea. This creates "thermal pollution". This changes the temperature of the receiving water, which causes both a physical change (e.g. reduction of dissolved oxygen) and a physiological change in fish and other animals.
Isolated Systems
Let us look at an isolated system. For an isolated system there is no heat (or work) entering or leaving, therefore Q = 0 and
In other words the total entropy must either increase or remain the same. Now consider an isolated system which contains two subsystems. If the entropy of one subsystem decreases, then entropy of the other subsystem must increase. Hence the total entropy of a system plus its surroundings must increase.
Two interesting consequences of this (more consequences are discussed in the following sections) are:
- This idea is behind the method used to get extremely low temperatures. Temperatures have be achieved down to 10-10 K.
- The method used is called adiabatic demagnetization and is as follows:
- Put the material in an insulated chamber.
- Introduce a magnetic field, which orients the molecules in line with the field.
- Reduce the temperature of the material to a low level by using, for example, liquid helium.
- The magnetic field is switched off. That causes the orientation of the molecules to again be random. Therefore, the entropy due to this orientation is increased.
- The changing of the magnetic field is considered to be very close to reversible, and since it is an isolated system, the total entropy change must be zero.
- Since the total entropy remains zero and the entropy due to the molecule orientation increases, the entropy due to the thermal energy must decrease. Hence, the temperature decreases.
- To get even lower temperatures, a variation called adiabatic nuclear demagnetization is used. This uses the nuclear magnetic moments instead of the molecular moments.
- If the universe is a closed system then the total entropy of the universe must increase. In other words its disorder would continue to increase until its death (called a heat death). The real question here, however, is "is the universe is really closed?"
Life and Order
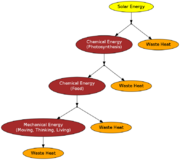
Life involves taking smaller units such as amino acids or glucose and creating larger units such as proteins and starch. These are then further put together to form structures such as skin or muscle. In other words it involves creating order. Hence, it reduces the entropy.
From above, since life reduces entropy, the entropy of the environment must increase.
Figure 3 shows how energy is transformed as is flows through a simplified biological system. The ultimate source of all energy in living systems is solar energy[4]. This energy is then converted to chemical energy through photosynthesis. This is then converted to food, which is then converted to mechanical energy for thinking, moving, and doing other functions.
Food Chains
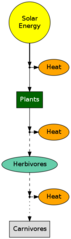
A good example of the effects of the second law and efficiencies is the transfer of energy within the food chain. Only about 5 – 20% of the energy is transferred from one level to the next. In other words 80 – 95% of the energy is lost as heat.
Figure 4 shows how energy flows through a food chain. Energy in food cains/webs is usually measured in units of energy per area per time (for example, kJ per m2 per year). Carnivores have only about 1-2% of the energy that plants capture. This explains why there are so many more plants than animals and why there are few predators then there are prey.
Perpetual Motion Machines
A perpetual motion machine is is literally a machine which is supposed to continue forever. There are two types: A perpetual motion machine of the first type (PMM1) is machine that claims to create, instead of conserving, energy. It violates the first law of thermodynamics. A perpetual motion machine of the second type (PMM2) is a machine that claims to violate the second law of thermodynamics. (There is also a perpetual motion machine of the third type (PMM3) - which are not related to thermodynamics, but rather supposedly has no dissipation of energy).
PMM2 attempt to convert heat completely to work. They produce work solely by cooling of a body. Hence, no heat is released from the machine. In other words, whereas a heat engine has two heat reserviors (one which is cooled and the other heated), a PMM2 has only one reservior (the one cooled).
All perpetual motion machines are inconsistent with the laws of thermodynamics and therefore cannot exist.
A good article on perpetual motion machines can be found on Wikipedia
No Hope
Remember this quote whenever you here about perpetual motion machines or another dubious statements:
The second law of thermodynamics holds, I think, the supreme position among laws of nature...If your theory is found to be against the second law of thermodynamics, I can give you no hope.
- Arthur S. Eddington
Continuing
The next three sections will:
- *Prove the Carnot principle: Carnot Principle - motivation
- Give example of the use of the Carnot cycle to solve cycle problems: Carnot Principle - example
- *Show the equivalence of the second law statements: Equivalence
- *Briefly give some additional statements of the second law: Other Statements|
- Describe the Third Law of thermodynamics: Third Law
The starred topics can be skipped without losing any continuity. All sections can be done in any order.