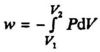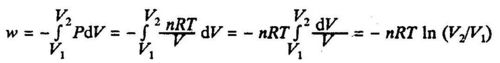The1stLawofThermodynamicsLesson1
Contents
THE FIRST LAW OF THERMODYNAMICS
This lesson deals with the exchange of energy betweeen a system and the surroundings. We shall only apply the first law to closed systems. The system receives energy in the form of heat and work from the surroundings.
The internal energy, U, the enthalpy, H, and the heat capacities, Cvand Cp will be defined, and equations are developed involving these state functions.
The pressure - volume work is studied for a reversible isothermal expansion of an ideal gas. The reversible isothermal expansion and the reversible adiabatic expansion of an ideal gas are compared.
Finally we shall consider an irreversible adiabatic expansion of a real gas, the Joule - Thomson experiment.
ENERGY, HEAT AND WORK
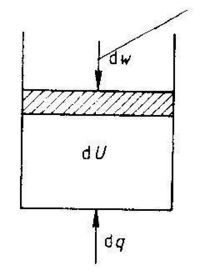
The first law of thermodynamics is a statement of the conservation of energy. The first law states that the internal energy of a system is a property of the system (a state function), and that changes in the internal energy, dU, results from the sum of energy added in the form of heat, dq, and work, dw.
dU = dq + dw (1.1)
It is very important, however, to notice that the first law does not rely 00, or specify in any way, the manner in which energy is stored in a system.
We can only measure the heat received by the surroundings, -dq, and the work performed on the surroundings, -dw. We can visualize the first law as shown in Fig. 1.1.
The first law in the present form is valid for a closed system.
Equation (1.1) is a postulate. It cannot be derived. The first law contains a second postulate in addition to eq. (1.1):
Energy is a state function
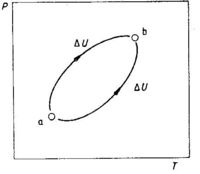
The chief criterion of a state function is that the change in a state function depends only on the final and initial state without regard to the process or pathway by which this change is made. The change in internal energy upon a change in state is equal to the internal energy of the final state minus the internal energy of the initial state, see Fig. 1.2:
ΔU = Ub - Ua (1.2)
This is a formulation of a second postulate.
The states a and b (see Fig. 1.2) represent two equilibrium states of a system (e.g. a gas where temperature and pressure are fixed). Each state can be described by the state variables P and T. The change in internal energy, ΔU, is independent of the path from a to b. A direct consequence of U being a state function is that we obtain ΔU = 0 when we go by one path from a to b and return by another path in a cyclic process. When the system is back to the initial state, the total change in the energy of the system is equal to zero. This can be expressed as
∮dU = 0 (1.3)
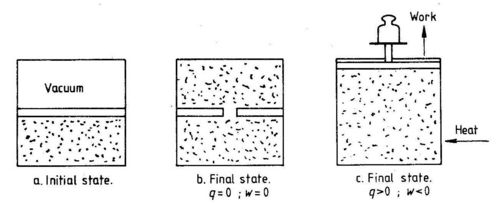
The integral of dU over a cyclic process is zero. The quantities q and w are not state functions. It is sufficient to show this by one example. We shall consider the isothermal (constant temperature) expansion of an ideal gas, see Fig. 1.3.
In the initial state (a) we~ave two equal volumes, one empty and one filled with gas. The final state of having the gas evenly distributed over both volumes can be obtained in two ways. One can make a hole in the separation wall and let the gas expand (b). In this case both heat and work are equal to zero. The same final state can be obtained by an arrangement where the gas performs mechanical work on the surrounding (work supplied to the system is negative). Heat is supplied to the gas to keep temperature constant (c). Although the final state is the same in both cases (also the initial state), heat and work supplied to the system are different in the two cases.
Pressure - Volume Work
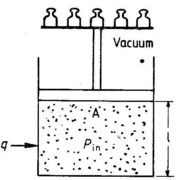
In thermodynamic calculations we frequently have to calculate the work supplied to a system when its volume changes. The system could be a gas, a liquid or a solid. To simplify calculations, let us assume that the system is contained in a cylinder with a frictionless piston as shown in Fig. 1.4.
For the system shown in Fig. 1.4 the pressure inside the system, Pin is very closed to being balanced by a weight, or a force, on the piston area, A, corresponding to an external pressure, Pex ≈ force/A. If Pex is less than Pin by an infinitesimal value, the piston will move upwards an infinitesimal distance, dl. The work supplied to the system, dw, is negative:
dw = - force x dl = - PexAdl = - PexdV
where dV is the change in volume. Since Pex ≈ Pin, we can write dw ≈ -PindV, or just:
dw ≈ -PdV(1.4)
During an isothermal expansion the internal pressure will decrease. If we adjust the external pressure to be very close to the internal pressure all the time (by removing the small weights pictured in Fig. 1.4, one by one), the integral work supplied will be:
In order to keep the temperature constant, heat must be supplied to the system during the expansion. All steps in the process can be balanced (Pex ≈ Pin), which means that the expansion can be performed in a reversible way.
If the system is an ideal gas (PV = nRT), we have:
where V1 and V2 are the initial and final volumes respectively.