How to run an independent samples t test analysis in SPSS

For two independent samples, we need at least two columns in the dataset: one column to contain a grouping variable (the explanatory variable) and another column to contain the test variable that will be compared (the response variable). The grouping variable can be numeric or string (e.g., 1 or 2, A or B, male or female), although beware of included spaces if variable set as string. The number of rows should be equal to the total number of observations in the study (i.e., n₁+n₂).

• Select Analyze > Compare Means > Independent-Samples T Test...

The Independent-Sample T Test dialog displays.

• Select the quantitative (measurement level=scale) response variable and use the arrow button to move it to the Test Variable(s) window.
• Select the categorical (measurement level=nominal or ordinal) explanatory variable and use the arrow button to move it to the Grouping Variable window.
• Click on the Define Groups... button under the Grouping Variable window.

The Define Groups dialog opens. The Group 1 and Group 2 values are the data values for the grouping variable that indicates membership in group 1 or group 2. (For example, if the variable Sex in the dataset is coded 1 (meaning male) and 2 (meaning female), entering a 1 for Group 1 indicates that Group 1 is the male group. Note that the difference in means is calculated as Group 1 - Group 2.

• Enter a value for Group 1.
• Enter a value for Group 2.
• Click OK.

• Select the Options button.

The Independent-Samples T Test Options dialog displays.

• Enter the desired confidence level.
• Click Continue.

The independent samples t test is fully specified.

• Click OK to run the analysis.

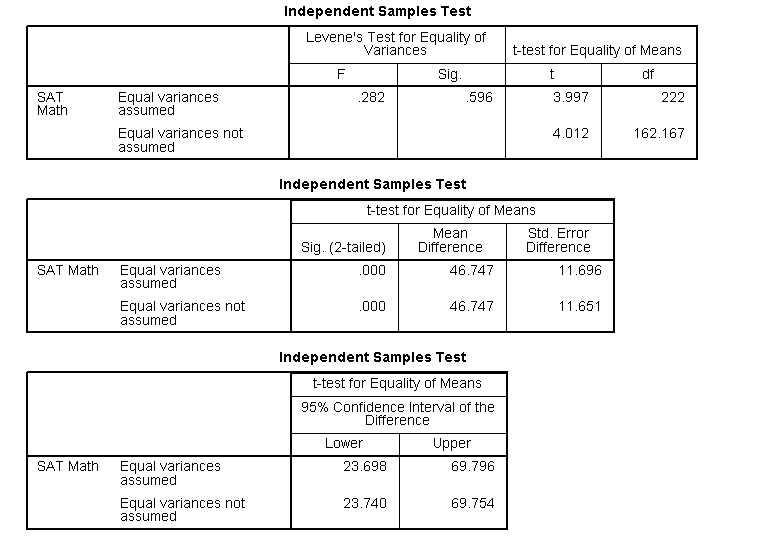
The image below displays a portion of the output for a t test of SAT Math scores comparing male and female computer science students. A few notes:

1. The analysis results for "Equal variances not assumed" uses the general t test method, which approximates a t distribution. The results for "Equal variances assumed" uses the pooled t test method, which has exactly a t distribution. The "Equal variances NOT assumed" is the generally preferred method, given the difficulty of assuring equal variances.
2. The t procedure for "Equal variances not assumed" is particularly robust when the sizes of the two samples are equal and the distributions of the two populations have similar shape, even when sample sizes are small. For situations when the populations have different shapes, larger samples are needed.