Random variables/Self-check assessment

Use the following quiz questions to check your understanding of random variables. Note that as soon as you have indicated your response, the question is scored and feedback is provided. As feedback is provided for each option, you may find it useful to try all of the responses (both correct and incorrect) to read the feedback, as a way to better understand the concept.

Introduction

Discrete vs. Continuous

Consider an elementary school student chosen at random. Indicate whether each of the following is a continuous or discrete random variable.

• The student's height: continuous
• The number of people in the student's family, including the student: discrete
• The number of books the student carried to school that morning: discrete
• The time it took the student to get to school that morning: continuous

Discrete random variables

Discrete probability distributions

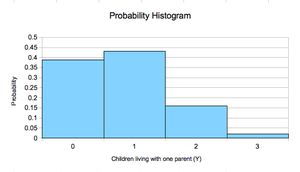
The 2010 US census reports that 27% of children live with one parent. Three US children are chosen at random, such that each has probability of .27 of living with one parent and each of the three children are chosen independently of the others. The random variable Y is the number of children chosen who live with one parent.

• What is the sample space (all of the particular outcomes from choosing 3 children)? (Use O for living with one parent and P for living with two parents or no parents)
  • There are 8 possible outcomes: PPP, PPO, POP, OPP, POO, OPO, OOP, OOO.
• What are the probabilities of each outcome?
  • Using the multiplication rule for independent events
    • For PPP: .73*.73*.73 = .389
    • For each of PPO, POP, OPP: .73*.73*.27 = .144
    • For each of POO, OPO, OOP: .73*.27*.27 = .053
    • For OOO: .27*.27*.27 = .020
• What value of Y corresponds with each outcome?
  • For PPP, Y = 0
  • For PPO, POP, OPP, Y = 1
  • For POO, OPO, OOP, Y = 2
  • For OOO, Y = 3
• What are the probabilities for each value of Y?
  • P(Y=0) = .389
  • P(Y=1) = .144 + .144 + .144 = .432 (using the addition rule for disjoint events)
  • P(Y=2) = .053 + .053 + .053 = .159 (using the addition rule for disjoint events)
  • P(Y=3) = .020
• Using paper and pencil sketch the probability histogram for the random variable Y.

Discrete probability distributions

The table below shows the probability distribution of Advanced Placement scores from the Spring 2011 tests. A 2011 test-taker is chosen at random; let the random variable X be the student's numerical score on the test. A passing score is a score of 3 or higher.

• What is the probability that the test-taker passed the test? .588 (to three decimals)
  • That's correct. As 3 is the passing score, we want the probability that the student scored a 3 or better. The desired probability is P(X >= 3) = P(X = 3) + P(X = 4) + P(X = 5) = .250 + .214 + .124 = .588
  • That's not quite right. As 3 is the passing score, we want the probability that the student scored a 3 or better. The desired probability is P(X >= 3). Try again.
• What is the probability that the test-taker scored at most 3? .662 (to three decimals)
  • That's correct. We want P(at most a score of 3). At most means that number or less. P(X ≤ 3) = P(X = 1) + P(X = 2) + P(X = 3) = .236 + .176 + .250 = .662.
  • That's not quite right. We want P(at most a score of 3). At most means that number or less: P(X ≤ 3). Try again.

Value of X	5	4	3	2	1
Probability	.124	.214	.250	.176	.236

Continuous random variables

Standard Normal distribution

• A standard Normal distribution has:
  • a mean of 1 and a standard deviation of 1.
    • That's not quite right. The distribution of z-scores is a standard Normal distribution. What is the z-score for the mean of the distribution? Try again.
  • a mean of 0 and a standard deviation of 1.
    • That's correct. The standard Normal distribution is defined as a Normal distribution with a mean of 0 and a standard deviation of 1: N(0,1).
  • a mean larger than its standard deviation.
    • That's not quite right. The distribution of z-scores is a standard Normal distribution. What is the z-score for the mean of the distribution? Try again.
  • all scores within one standard deviation of the mean.
    • That's not quite right. The standard Normal distribution is bell-shaped with about 99.7% of scores within 3 standard deviations. The distribution of z-scores is a standard Normal distribution. Try again.
• A number 1.5 standard deviations below the mean has a z-score of:
  • 1.5
    • That's not quite right. You are correct that a z-score is equal to the number of standard deviations below or above the mean. Think about what z-score values occur below the mean. Try again.
  • -1.5
    • That's correct. A z-score is equal to the number of standard deviations below or above the mean. Numbers below the mean have negative z-scores.
  • 3
    • That's not quite right. A z-score indicates the number of standard deviations below or above the mean. Try again.
  • more information is needed
    • That's not quite. As a z-score indicates the number of standard deviations below or above the mean, in fact there is enough information to determine the z-score. Try again.

Standardized scores

In an article in the Journal of American Pediatric Health researchers claim that the weights of healthy babies born in the United States form a distribution that is nearly Normal with an average weight of 7.25 pounds and standard deviation of 1.75 pounds.

• Baby Alice's weight at birth was 8.50 pounds. What is her z-score?
  • 8.50
    • That's not quite right. 8.50 is Alice's weight at birth in pounds. Recall that the z-score of a Normal value is (value - mean)/standard deviation. Try again.
  • 1.25
    • That's not quite right. It seems that you have calculated the difference between baby Alice's weight and the mean. Recall that the z-score of a Normal value is (value - mean)/standard deviation. Try again.
  • -.71
    • That's not quite right. It seems that you may have calculated: (mean - value) / standard deviation. The mean and value are backwards. Note that the z-score of a Normal value is (value - mean)/standard deviation. Try again.
  • .71
    • That's correct. Baby Alice's z-score is (8.50 - 7.25)/1.75 = .71
• The fact that baby Alice's z-score is .71, tells us that her weight is
  • .71 pounds above the mean
    • That's not quite right. A z-score tells us how many standard deviations above or below the mean the value is. Positive z-scores indicate that the value is above the mean, and negative z-scores indicate that the value is below the mean. Try again.
  • .71 standard deviations above the mean
    • That's correct. A z-score of .71 indicates that baby Alice's weight of 8.5 pounds is .71 standard deviations above the mean.
  • .71 pounds below the mean
    • That's not quite right. A z-score tells us how many standard deviations above or below the mean the value is. Positive z-scores indicate that the value is above the mean, and negative z-scores indicate that the value is below the mean. Try again.
  • .71 standard deviations below the mean
    • That's not quite right. Recall that positive z-scores indicate that the value is above the mean, and negative z-scores indicate that the value is below the mean. Try again.
• Baby Peter was born the same night as baby Alice. The z-score for baby Peter's weight is -2.33. This means that baby Peter's weight is
  • much lower than average
    • That's correct. Baby Peter's z-score indicates that his score is 2.33 standard deviations below the mean, which is well below average. In particular, from the standard deviation rule, we know that, since baby Peter's weight is less than 2 standard deviations below the mean, his weight is in the lowest 2.5% of birth weights.
  • slightly lower than average
    • That's not quite right. Although baby Peter's weight is below average, his z-score indicates that his weight is 2.33 standard deviations below the mean, which is much below average. In particular, from the standard deviation rule, we know that, since baby Peter's weight is less than 2 standard deviations below the mean, his weight is in the lowest 2.5% of birth weights.
  • slightly higher than average
    • That's not quite right. A negative z-score indicates that the value is below the mean. Try again.
  • much higher than average
    • That's not quite right. A negative z-score indicates that the value is below the mean. Try again.
• Baby Peter's actual birth weight, given a z-score of -2.33, was
  • 11.32 pounds
    • That's not quite right. Baby Peter's z-score of -2.33 indicates that his score is 2.33 standard deviations below the mean. It seems like you added 2.33 standard deviations to the mean rather than subtracting. Try again.
  • 9.58 pounds
    • That's not quite right. Baby Peter's z-score of -2.33 indicates that his score is 2.33 standard deviations below the mean. It seems like you added (rather than subtracted) 2.33 points (rather than standard deviations. Try again.
  • 3.17 pounds
    • That's correct. Baby Peter's z-score of -2.33 indicates that his score is 2.33 standard deviations below the mean. As the mean is 7.25 and each standard deviation is 1.75, we can solve for the value in the z-score equation: z = (value - mean)/standard deviation; -2.33 = (value - 7.25)/1.75; value = (-2.33)(1.75) + 7.25 = 3.17.
  • 4.92 pounds
    • That's not quite right. Baby Peter's z-score of -2.33 indicates that his score is 2.33 standard deviations below the mean. It seems like you subtracted 2.33 points from the mean rather than 2.33 standard deviations. Try again.
• The US Department of Health classifies a newborn as "low birth weight" if her/his weight is less than 5.5 pounds. What is the probability that a baby, chosen at random, weighs less than 5.5 pounds?
  • About .16
    • That's correct. The first step in finding the area under curve is to calculate the z-score: Z = (5.5 - 7.25)/1.75 = -1. A z-score of -1 means that the value is one standard deviation below the mean, and we can use the standard deviation rule to determine the area under the curve: P(Z < -1). The standard deviation rule says that 68% of the values occur between one standard deviation above and one standard deviation below the mean. That means that 32% of the values occur below and above that range. P(Z < -1) is only the lower portion: (1/2)*.32 = .16
  • About .84
    • That's not quite right. This is the probability that the baby's weight is less than 1 standard deviation above the mean P(Z < 1). Recall that the z-score of a Normal value is (value - mean)/standard deviation. Consider how the resulting z-score relates to standard deviations above or below the mean, and whether the standard deviation rule can be used. Try again.
  • About .10
    • That's not quite right. The first step in finding the area under curve is to calculate the z-score. Then consider how the resulting z-score relates to standard deviations above or below the mean, and whether the standard deviation rule can be used. Try again.
  • the probability cannot be determined
    • That's not quite right. The first step in finding the area under curve is to calculate the z-score. Then consider how the resulting z-score relates to standard deviations above or below the mean, and whether the standard deviation rule can be used. Try again.

Standardized scores

Use either a Normal probability calculator, standard or inverse, or Table A in the text to determine the specified probabilities.

• What is the probability that a Normal random variable will take a value that is less than 1.15
  • .8749
    • That's correct. As P(Z < 1.15) is the area to the left of the z-score, the probability is the entry in the Standard Normal Probabilities table for z = 1.15, which is .8749.
  • .1251
    • That's not quite right. As P(Z < 1.15) is the area to the left of the z-score, the probability is the entry in the Standard Normal Probabilities table for z = 1.15. It may be that you either obtained the probability for a z-score below -1.15, or that you subtracted the table entry for 1.15 from 1. Try again.
  • .9332
    • This is not quite right. As P(Z < 1.15) is the area to the left of the z-score, the probability is the entry in the Standard Normal Probabilities table for z = 1.15. It may be that you obtained the probability for z = 1.5 by mistake. Try again.
  • .0668
    • This is not quite right. As P(Z < 1.15) is the area to the left of the z-score, the probability is the entry in the Standard Normal Probabilities table for z = 1.15. It may be that you obtained the probability for z = -1.5 by mistake. Try again.
• What is the probability that a Normal random variable will take a value that is between 2.5 standard deviations below the mean and 1.5 standard deviations above the mean? In other words, what is P(-2.5 < Z < 1.5)?
  • .9332
    • That's not quite right. .9332 is just P(Z < 1.5). Note that P(a < Z < b) = P(Z < b) - P(Z < a), the probability of a z-score less than a subtracted from the probability of a z-score less than b. Try again.
  • .0062
    • That's not quite right. .0062 is just P(Z < -2.5). Note that P(a < Z < b) = P(Z < b) - P(Z < a), the probability of a z-score less than a subtracted from the probability of a z-score less than b. Try again.
  • .9270
    • That's correct. P(-2.5 < Z < 1.5) = P(Z < 1.5) - P(Z < -2.5) = .9332 - .0062 = .9270.
  • .8664
    • That's not quite right. Note that P(a < Z < b) = P(Z < b) - P(Z < a), the probability of a z-score less than a subtracted from the probability of a z-score less than b. Try again.
• What is the probability that a Normal random variable will take a value that is more than 2.33 standard deviations above its mean? In other words, what is P(Z > 2.33)?
  • .9898
    • That's not quite right. It may be that you obtained the probability of a z-score less than 2.32, rather than greater than 2.33. The Standard Normal Probabilities table provides the probabilities for less than the z-score. Consider that by symmetry of the z curve centered on 0, P(Z > +2.33) = P(Z < -2.33). Also, because the total area under the Normal curve is 1, P(Z > +2.33) = 1 - P(Z < 2.33). Try again.
  • .9901
    • That's not quite right. .9901 is P(Z < 2.33), and we are looking for P(Z > 2.33). The Standard Normal Probabilities table provides the probabilities for less than the z-score. Consider that by symmetry of the z curve centered on 0, P(Z > +2.33) = P(Z < -2.33). Also, because the total area under the Normal curve is 1, P(Z > +2.33) = 1 - P(Z < 2.33). Try again.
  • .0102
    • That's not quite right, but very close. Check to be sure you used the correct z-score: z = 2.33. Try again.
  • .0099
    • That's correct. P(Z > 2.33) = P(Z < -2.33) = .0099 or, P(Z > 2.33) = 1 - P(Z < 2.33) = 1 - .9901 = .0099.

Inverse Normal calculations

• The probability is .33 that a standardized Normal variable takes a value above what particular value of z? In other words, what is the value of z that satisfies P(Z > z) = .3300? .44
  • That's correct. P(Z > .44) = .3300.
  • That's not quite right. You are given the probability and are asked to provide a z-value, so you start by finding the probability in the body of the table, and then use the row and column headings to determine the z-score. Note that the Standard Normal Probabilities table provides the probabilities for less than the z-score, but this problem looks at the probability of a score greater than the z-value. Try again.

Means and variances of random variables

Mean of a discrete random variable

• The number of times during the work/school week (Monday to Friday) that the Willow family eats dinner together varies. Use the following probability distribution to find the typical number of days that the Willow family eats together. μ_W = 3.08 (to two decimals)
  • That's correct. μ_W = 0(.02) + 1(.08) + 2(.20) + 3(.25) + 4(.40) + 5(.05) = 3.08.
  • That's not quite right. Recall that the mean of a random variable is the weighted average: multiply each possible value by its probability, and then add all of the resulting products. Try again.
• The number of times during the work/school week (Monday to Friday) that the Youmans family eats dinner together is shown in the probability distribution below. The values for the W and Y distributions are the same, but the distribution of probability differs. Using just a visual comparison of the two distributions, we would expect the mean of W to be greaterthan (greaterthan, lessthan, aboutequalto) the mean of Y.
  • That's correct. In the probability distribution for W the larger values (3, 4, and 5) have most of the weight (70%), while in the probability distribution for Y the smaller values (0, 1, and 2) have most of the weight (80%). Given that the mean is the average of the values weighted by their probabilities, we would expect the mean of W to be greater than the mean of Y.
  • That's not quite right. Note that in the probability distribution for W the larger values (3, 4, and 5) have most of the weight (70%), while in the probability distribution for Y the smaller values (0, 1, and 2) have most of the weight (80%). Recall that the mean is the average of the values weighted by their probabilities. Try again.
• The mean of Y (the average times per week that the Youmans family eats together) is 1.92 (to two decimals).
  • That's correct. μ_Y = 0(.10) + 1(.20) + 2(.50) + 3(.10) + 4(.08) + 5(.02) = 1.92.
  • That's not quite right. Recall that the mean of a random variable is the weighted average: multiply each possible value by its probability, and then add all of the resulting products. Try again.
• The Zinn family eats together on average 2.5 times per week, with a standard deviation of 2.05. Caroline Zinn says that her family eats together 4 times in a work/school week on a regular basis. Given μ_Z = 2.5 and σ_Z = 2.05, is Caroline's statement believable? Why?
  • Yes, as the mean number of times the Zinn family eats together is 2.5 and the standard deviation is 2.05, eating together 4 times per week is less than one standard deviation above the mean: μ_Z + 1σ_Z = 2.5 + (1)2.05 = 4.55. Caroline is right, the Zinn family eating together 4 times per week is a rather common occurrence.

How often the Willow family eats together during the week (W)

Value of W	0	1	2	3	4	5
Probability	.02	.08	.20	.25	.40	.05

How often the Youmans family eats together during the week (Y)

Value of Y	0	1	2	3	4	5
Probability	.10	.20	.50	.10	.08	.02

Rules for means, standard deviations and variances of random variables

Young women's heights in the US are Normally distributed with mean μ_X = 64.5 inches and standard deviation σ_X = 2.5 inches. We would like to compare the heights of US women to the heights of Australian women: μ_Z = 163.9 centimeters and standard deviation σ_Z = 6.6 centimeters. We can use the rules for a linear transformation to convert the US statistics to centimeters (note: 2.54 cm = 1 inch).

• μ_2.54X = 163.8 centimeters (to one decimal)
  • That's correct. Applying the linear transformation rule, μ_{a + bX} = a + b μ_X, we can calculate μ_2.54X = (2.54)(μ_X) = (2.54)(64.5) = 163.8. We conclude that the mean heights of young women in the US and Australia are quite similar.
  • That's not quite right. Recall that the linear transformation rule for a mean is μ_{a + bX} = a + b μ_X. Note that when converting from inches to centimeters there is no constant (a), only the multiplier (b), which in this situation is 2.54. Try again.
• σ_2.54X = 6.4 centimeters (to one decimal)
  • That's correct. Applying the linear transformation rule for the variance, σ²_{a + bX} = b² σ_X², we can calculate [math]\sigma_{2.54X}^2 = (2.54^2)(\sigma_X^2) = (2.54^2)(2.5^2) = 40.32[/math]. The standard deviation is the square root of the variance, [math]\sigma_{2.54X} = \sqrt{\sigma_{2.54X}^2} = \sqrt{40.32} = 6.4[/math]. Not surprisingly the standard deviation of heights for young women in the US and Australia are quite similar.
  • That's not quite right. Recall that the linear transformation rule for a variance is σ²_{a + bX} = b² σ_X². Note that this rule applies only to variances; the standard deviation is the square root of the variance. Try again.

Rules for means, standard deviations and variances of random variables

The bedtine routine for many families with young children can be sectioned into two parts 1) taking a bath, getting pajamas on, brushing teeth, etc. (bath time) and 2) reading a story (reading time). In one family the bath time has a mean of 15 minutes and a standard deviation of 12 minutes. The reading time has a mean of 20 minutes and a standard deviation of 8 minutes. The bath time and the reading time are negatively correlated: ρ = -0.3.

• The mean time to complete the entire bedtime routine is
  • less than 35 minutes since the negative correlation tells you that more time spent in one part will be associated with less time spent in the other part.
    • That's not quite right. The rule for combining means for two random variables, X and Y, is μ_X+Y = μ_X + μ_Y. Note that the correlation is not used in the calculation. The correlation affects the variability of the total time, not the mean. Try again.
  • 35 minutes.
    • That's correct. The rule for combining means for two random variables, X and Y, is μ_X+Y = μ_X + μ_Y. If X is the bath time and Y is the reading time, then the mean time to complete the entire bedtime routine is μ_X+Y = μ_X + μ_Y = 15 + 20 = 35 minutes. The correlation does not change the mean of X + Y, although it does affect its standard deviation.
  • greater than 35 minutes since the measurements are correlated which raises the mean regardless of the sign of the correlation.
    • That's not quite right. The rule for combining means for two random variables, X and Y, is μ_X+Y = μ_X + μ_Y. Note that the correlation is not used in the calculation. The correlation affects the variability of the total time, not the mean. Try again.
• When calculating the standard deviation (variability) of the sum of bath time and reading time we need to keep in mind that: (check all that apply)
  • the two random variables, bath time and reading time, are independent.
    • That's not quite right. When two random variables are independent, their correlation is 0; knowing something about one variable tells you nothing about the other variable. Try again
  • the two random variables, bath time and reading time, are dependent.
    • That's correct. A non-zero correlation indicates that two random variables are dependent. The variability of the sum of two random variables depends on the correlation between them as well as the variability of each individual variable.
  • the calculation of the variance of the sum of bath time and reading time is simply the addition of the variance of bath time plus the variance of reading time.
    • That's not quite right. The variance of the sum of two dependent random variables is more than the addition of the variances of each individual variable; the correlation between them impacts the overall variability. Try again.
  • the standard deviations for two random variables cannot be directly added in order to obtain the standard deviation of their sum.
    • That's correct. To combine two standard deviations, use the general addition rule for variances of random variables: [math]\sigma^2_{X+Y} = \sigma^2_X + \sigma^2_Y + 2 \rho \sigma_X \sigma_Y[/math]. Don't forget to take the square root of the result to get back to the standard deviation.
  • the variance of the sum of two random variables depends on the correlation between them as well as the variances of each variable.
    • That's correct. To calculate the variance of the sum, we use the general addition rule for variances of random variables: [math]\sigma^2_{X+Y} = \sigma^2_X + \sigma^2_Y + 2 \rho \sigma_X \sigma_Y[/math], the third term of which includes the correlation ρ. When the two random variables are independent, their correlation is 0, and this term of the equation drops out.
• The standard deviation of the time required to complete the entire bedtime routine is
  • 14.4 minutes.
    • That's not quite right. As the standard deviation is the square root of the variance, we can use the general addition rule for variances of random variables: [math]\sigma^2_{X+Y} = \sigma^2_X + \sigma^2_Y + 2 \rho \sigma_X \sigma_Y[/math]. Recall that ρ is the population parameter for correlation. It seems like you have forgotten the correlation portion of the formula; calculating the standard deviation of X + Y as if the two variables were uncorrelated. Try again
  • 20 minutes
    • That's not quite right. As the standard deviation is the square root of the variance, we can use the general addition rule for variances of random variables: [math]\sigma^2_{X+Y} = \sigma^2_X + \sigma^2_Y + 2 \rho \sigma_X \sigma_Y[/math]. Recall that ρ is the population parameter for correlation. You may have forgotten to put the correlation into the formula, or just added the standard deviations. Try again.
  • 150.4 minutes
    • That's not quite right. As the standard deviation is the square root of the variance, we can use the general addition rule for variances of random variables: [math]\sigma^2_{X+Y} = \sigma^2_X + \sigma^2_Y + 2 \rho \sigma_X \sigma_Y[/math]. It seems like you forgot to take the square root of the variance of X + Y. Try again.
  • 12.3 minutes
    • That's correct. As the standard deviation is the square root of the variance, we can use the general addition rule for variances of random variables: [math]\sigma^2_{X+Y} = \sigma^2_X + \sigma^2_Y + 2 \rho \sigma_X \sigma_Y[/math]. If X is the bath time and Y is the reading time, then the variance of the time required to complete the entire bedtime routine is [math]\sigma^2_{X+Y} = \sigma^2_X + \sigma^2_Y + 2 \rho \sigma_X \sigma_Y = 12^2 + 8^2 +(2)(-.3)(12)(8) = 150.4[/math]. The standard deviation is [math]\sigma_{X+Y} = \sqrt{\sigma_{X+Y}^2} = \sqrt{150.4} = 12.3[/math].