FreeEnergyLesson5
LESSON 5: REAL GASES. PRESSURE DEPENDENCE OF GIBBS ENERGY. FUGACITY
The pressure dependence of Gibbs energy for one mole of an ideal gas, ΔG = RT ln (P/P°), was given by eq. (3.10). For a real gas we can calculate ΔG using dG = VdP if the volume is known as a function of pressure. It is more convenient, however, to replace the pressure of a real gas with the fugacity, f, which is defined by the equation:
ΔG = ΔG° + RT ln (f/P°) (5.1)
The standard state of a real gas is a hypothetical state in which the gas is at a pressuer P° = 1 bar and behaving as an ideal gas.
The fugacity may be considered as the effective pressure of the real gas. Real gases approach the behavior of ideal gases at low pressure, and the fugacity approaches the pressure when the pressure approaches zero:
(f/P) = 0 (5.2)
When we change the pressure from P1 to P2 for one mole of a real gas, the change in Gibbs energy is:
ΔG =ΔG 2 -ΔG 1 = RT ln (f 2 / f 1 )
The same change in Gibbs energy can be expressed as ΔG =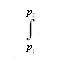 
VdP in agreement with eq. (3.7), and hence:
RT ln (f2 / f 1 ) = 
VdP
Adding and subtracting the same term RT/P in the integral we obtain:
RT ln (f 2 /f 1 ) = 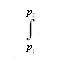(RT/P + (V – RT/P)) dP = RT ln 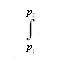+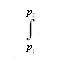(V- RT/P) dP
Rearranging the equation we obtain:
RT ln (f2/P2)/(f1/P1) = 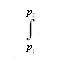(V - RT/T)dP (5.3)
When P2 = P and P1 → 0 we use eq. (5.2) and obtain:
RT ln (f/P) = 
(V - RT/P) dP (5.4)
The compressibility factor Z was used to describe the P, V, T relations for a real gas. We may rearrange the eq. Z = PVm/RT to express the volume of one mole of a real gas by R, P, T and Z:
V = (RT/P) Z (5.5)
Introducing this expression in eq. (5.4) we obtain:
RT ln (f/P) =
(RT/P Z - RT/P) dP
OR
RT ln (f/P) = p)(Z-1) dP/P (5.6)
This equation can be used to find the ratio f/P, when Z is known as a function of P.
Several modem industrial processes operate at very high pressures, and calculations for real gases are needed. The equilibrium constant may be expressed by fugacities:
K = 
i (fi/ P°)vi (5.7)
The fugacity, fi, of the gas Bi may be written as the product of a fugacity coefficient, 
i and the partial pressure Pr,
fi = 
i Pi (5.8)
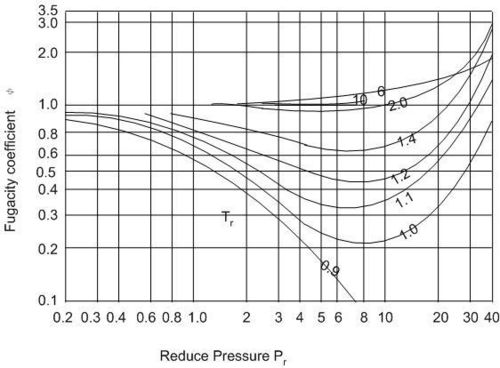
The fugacity coefficient as a function of reduced pressure, Pr, is approximately the same for all gases, see Fig. 5.1, which may be used to find values of for any gas.
THE MAXWELL RELATIONS
The fundamental equation for a closed system, dU = TdS - PdV, eq. (5.15), was derived in lesson 3. It can be combined with the definitions of H, A and G to give a number of relations between these quantities and the variables, P, T, V and S. Expressions for H, A and G have been given earlier:
H= U+PV (5.9)
A=U-TS (5.10)
G=U+PV-TS (5.11)
The differentials of these equations are
dH = dU + PdV + VdP (5.12)
dA = dU - TdS - SdT (5.13)
dG = dU + PdV + VdP - TdS - SdT (5.14)
From these three equations we may eliminate dU by means of eq.(5.15). In addition to eq. (5.13) we have three differentials:
dU= TdS -PdV (5.15)
dH= TdS + VdP (5.16)
dA = - SdT - PdV (5.17)
dG = - SdT + VdP (5.18)
From the four differentials above we can derive four relations, called the Maxwell relations.
We shall show the procedure for the derivation using eq. (5.15).
Since U is a single-valued function of S and V, we have:
dU = (∂U/∂S)vdS + (∂U/∂V)s dV (5.19)
Comparing eqs (5.19) and (5.15) we see that:
(∂U/∂S)v = T (5.20)
(∂U/∂V)s = -P (5.21)
According to Euler's reciprocity theorem for exact differentials (e.g., the derivative of a state function), the order of differentiation does not matter. Hence:
∂sU / ∂S∂V = ∂sU/ ∂V∂S (5.22)
Applying eq. (5.22) to the two differentials eqs (5.20, 5.21), we obtain the first Maxwell relation:
( ∂T/∂V)s = - (∂P/∂S)v (5.23)
The other three Muwell relations are derived in a similar way from eqs (5.16, 5.17, 5.15):
(∂T/∂P)s = (∂V/∂S)p (5.24)
(∂S/∂V)T = (∂P/∂T)v (5.25)
-(∂S/∂P)T = (∂V/∂T)P (5.26)
The two last equations are particularly useful because we can use them to find the change in entropy with volume and pressure respectively at constant temperature when the equation of state (the P, V, T relation) is known.
