Basics of Solar Radiation
Contents
SOLAR RADIATION BASICS
INTRODUCTION
Solar radiation is a term used to describe visible and near-visible (ultraviolet and near-infrared) radiation emitted from the sun. The different regions are described by their wavelength range within the broad band range of 0.20 to 4.0 µm (microns). Terrestrial radiation is a term used to describe infrared radiation emitted from the atmosphere. The following is a list of the components of solar and terrestrial radiation and their approximate wavelength ranges:
- Ultraviolet: 0.20 - 0.39 µm
- Visible: 0.39 - 0.78 µm
- Near-Infrared: 0.78 - 4.00 µm
- Infrared: 4.00 - 100.00 µm
On the surface of the earth on a clear day, at noon, the direct beam radiation will be approximately 1000 watts/meter2 for many locations.
The availability of energy is affected by location (including latitude and elevation), season, and time of day. All of which can be readily determined. However, the biggest factors affecting the available energy are cloud cover and other meteorological conditions which vary with location and time.
|
The objective of the course is to enable students understand the basics of solar radiation. |
EXTRATERRESTRIAL RADIATION
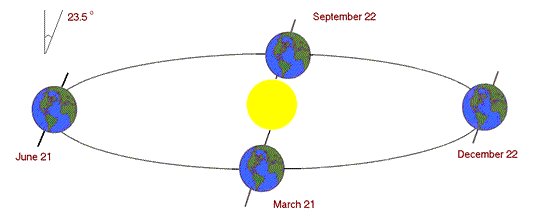
Solar radiation incident outside the earth's atmosphere is called extraterrestrial radiation. On average the extraterrestrial irradiance is 1367 Watts/meter2 (W/m2).
This value varies by ±3% as the earth orbits the sun. The earth's closest approach to the sun occurs around January 4th and it is furthest from the sun around July 5th. The extraterrestrial radiation is:
ZENITH, AZIMUTHAL, AND HOUR ANGLES
To describe the sun's path across the sky one needs to know the angle of the sun relative to a line perpendicular to the earth's surface—this is called the zenith angle (q)—and the sun's position relative to the north-south axis, the azimuthal angle (a). The hour angle (w) is easier to use than the azimuthal angle because the hour angle is measured in the plane of the "apparent" orbit of the sun as it moves across the sky. Since the earth rotates approximately once every 24 hours, the hour angle changes by 15 degrees per hour and moves through 360 degrees over the day. Typically, the hour angle is defined to be zero at solar noon, when the sun is highest in the sky.
SOLAR AND LOCAL STANDARD TIME
To describe the position of the sun in local standard time1, one needs to know the relationship between solar time and local standard time. Local time is the same in the entire time zone whereas solar time relates to the position of the sun with respect to the observer, and that is different depending on the exact longitude where solar time is calculated.
To adjust solar time for longitude: subtract (Longlocal – Longsm)/15 (hours) from the local time.
Where Longlocal is the longitude of the observer in degrees and Longsm is the longitude for the standard meridian for the observer's time zone.
EQUATION OF TIME
As the earth moves around the sun, solar time changes slightly with respect to local standard time. (This is mainly related to the conservation of angular momentum as the earth moves around the sun.)
This time difference is called the equation of time and can be an important factor when one is at sea, navigating by the sun or stars. It is also important when determining the position of the sun for solar energy calculations. An approximate formula for the equation of time (Eqt) in minutes is:
4.Eqt = -14.2 sin (p(n + 7) / 111)
for year day n between 1 and 106
5.Eqt = 4.0 sin (p(n - 106) / 59)
for year day n between 107 and 166
6.Eqt = -6.5 sin(p(n - 166) / 80) for year day n between 167 and 246
7.Eqt = 16.4 sin(p(n - 247) / 113)
for year day n between 247 and 365
Combining the longitude correction and the equation of time, the relationship between the solar time and local standard time is given by:
8.Tsolar = Tlocal + Eqt / 60 + (Longsm - Longlocal) / 15 (hrs)
Since equations use sine and cosine functions it is conceptually easier to calculate using the hour angle (w) instead of time.
The relationship between hour angle and time is:
9.w = p * (12 - Tsolar) / 12
THE HOUR ANGLE IS IN UNITS OF RADIANS.
With the above information, we can now calculate the cosine of the zenith angle:
10.cos(Z) = sin(l)sin(d) + cos(l)cos(d)cos(w)
where l is the latitude of the location of interest.
SUNRISE AND SUNSET TIMES
Sunrise and sunset occur when the sun is at the horizon and hence the cosine of the zenith angle is zero.
Setting the cosine of the zenith angle to zero in Equation 7 results in the following equation:
11.wsr,ss = arccos(-tan(l)tan(d))
where wsr is the sunrise hour angle and wss is the sunset hour angle.
The sunrise and sunset hour angles are not exactly the same value as the sunrise and sunset times that appear in the local paper. The sunrise reported here will be earlier and the sunset times will be later because the sunlight is refracted as it moves through the earth's atmosphere and the sun appears slightly higher in the sky than simple geometrical calculations indicate.
During the middle of the day the effect is small, but during the sunrise or sunset periods, the effect can change the apparent solar time by about 5 minutes.
GLOBAL, BEAM, AND DIFFUSE IRRADIANCE
Near noon on a day without clouds, about 25% of the solar radiation is scattered and absorbed as it passes through the atmosphere. Therefore about 1000 w/m2 of the incident solar radiation reaches the earth's surface without being significantly scattered. This radiation, coming from the direction of the sun, is called direct normal irradiance (or beam irradiance).
Some of the scattered sunlight is scattered back into space and some of it also reaches the surface of the earth. The scattered radiation reaching the earth's surface is called diffuse radiation. Some radiation is also scattered off the earth's surface and then re-scattered by the atmosphere to the observer. This is also part of the diffuse radiation the observer sees. This amount can be significant in areas in which the ground is covered with snow. [math]Y=x+2r+C[/math]