Basic Word Problems

As I wrote in the Word Problems page, many math students have problems with word problems. Perhaps that's why they are called word problems. To start with it is helpful to know how to translate English words into mathematical language. See http://www.purplemath.com/modules/translat.htm for some help with this.

Below is a three step approach that works for solving just about any word problem. Practice these steps and hopefully you won't have any more problems with word problems.

1. Translate the problem from English into math, using as many variables as it takes. Use variables that make sense. For example, use 't' for time and 'r' for rate. However, avoid variables that can be confused with numbers (e.g., s can be confused with 5).
2. Substitute from one equation into another. Once the problem has been translated into algebraic language, you will likely find you have too many variables. Take what one variable equals and substitute it into another equation.
3. Solve the equation you substituted into and then use that result in the other equation.

Here are some basic word problem example.

Example 1 -- Making Two Squares Out of a Piece of Wire Cut into Two Pieces

A length of wire 88 centimetres longs is cut into two pieces. Each of those two pieces is then bent into a square. The length of a side of the bigger square is 4 centimetres longher than the side of the smaller one. How should the wire be cut?

Visualize, or better yet, draw a piece of wire that has been cut into two pieces. We don't know the length of either piece. The two pieces of wire would look something like this.

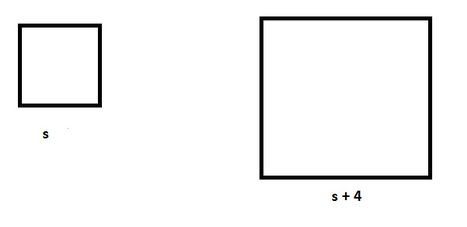
We then take these two wires and make a square out of each piece for a total of two squares of unknown sides. However, we do know the side of one is 4 centimetres longer than the side of the other. The squares would look something like this.

We are asked how the wire should be cut. That is how long is each piece of the cut wire. To find that that we have to figure out what the side of each square is.

Step 1 -- Translate

We need to know how to find the perimeter for the square. To do so, we simply add the four sides. Using variables that make sense, that translates to

P₁= perimeter of the first square

s₁ = side of the first square

So for the perimeter of the first square, the small square translates to

P₁ = 4s₁

The second larger square uses a variation of the same formula.

P₂= perimeter of the second square

s₂ = side of the second square

So for the perimeter of the second square, the small square translates to

P₂ = 4s₂

Then we translate "we do know the side of one is 4 centimetres longer than the side of the other." See the picture of the squares above for how we get that translation.

As the side of the large square is 4 metres longer, that translates to

s₂ = s₁ + 4

Finally we know that the length of the wire before it was cut was 88 centimetres long. That means the perimeter of the small square added to the perimeter of the large square is 88 centimetres. That translates to

P₁ + P₂ = 88

With the word problem translated, we are ready for step 2.

Step 2 -- Substitute

First we take the immediately above.

P₁ + P₂ = 88

Substituting in the formulas for finding the perimeter of each square into the translation, we get

4s₁ + 4s₂ = 88

We know the relationship between each of the two squares is

s₂ = s₁ + 4

so we can come up with our final substitution.

4s₁ + 4(s₁ + 4) = 88

Step 3 -- Solve

We can now solve to find the length of the side of the small triangle.

4s₁ + 4(s₁ + 4) = 88

That simplifies to

4s₁ + 4s₁ + 16 = 88

8s₁ + 16 = 88

8s₁ = 72

s₁ = 9

So the side of the small square is 9 centimetres.

Substitute that answer s₁ (9) into the equation for length of the side of the second square gets us

s₂ = s₁ + 4

s₂ = 9 + 4

s₂ = 13

So the side of the small square is 9 centimetres and the side of the large one is 13 centimetres.

Finally we need to remember that each square is made up of four sides. So the perimeter of the small square is

4 times 9 = 36

and the large square is

4 times 13 = 52

We can verify these answers by substituting them back into the original equation.

The two wires before they were cut we 88 cm long. Adding 36 and 52 does indeed get us 88.

Therefore we have solved the problem. We cut the 88 cm wire into one piece of 36 cm leaving us a second piece of 52 cm.

Example 2 -- Basketball Court

Visualize, or better yet, draw a basketball court that has a perimeter of 100 metres. We don't know the width or the length. However, we do know the length is 5 metres longer than twice the width. Find the length and width.

Step 1 -- Translate

Use variables that make sense.

P = perimeter

W = width

L = length

The appropriate translation is below each relevant part of the word problem.

a basketball court that has a perimeter of 100 metres translates to

P = 100

the length is 5 metres longer than twice the width translates to

L = 5 + 2W

You also need to know that the formula for calculating perimeter of a rectangle is

P = 2L + 2W

Step 2 -- Substitute

We start with the equation that has the most information

P = 2L + 2W

and then substitute what we know into the equation. We know that the perimeter is 100 metres so we can substitute 100 in for P.

100 = 2L + 2W

We also know that the length is 5 metres longer than twice the width so we can substitute that in for L

100 = 2(5 + 2W) + 2W

Now that we have an equation in one variable (W), we can solve for the width.

Step 3 -- Solve

What is the width of the basketball course? We know that

100 = 2(5 + 2W) + 2W

That simplifies to

100 = 10 + 4W +2W

100 = 10 + 6W

6W = 90

W = 15

So the width is 18 metres.

Substitute the width (18) into the other equation for length gets us

L = 5 + 2W

L = 5 + 2(15)

L = 35

So the width is 18 metres and the length is 41 metres.

We can verify these answers by substituting them back into the original perimeter equation.

P = 2L + 2W

100 = 2(35) + 2(15)

100 = 70 + 30

100 = 100

Therefore we have solved the problem.

Example 3 -- Midnight Snack

Two brothers are in bed for the night. One awakes and goes down to the kitchen for a snack. All that he find in the fridge is a bag of apples. He eats three-fourths of the apples and goes back to bed. Later the second brother awakes and eats three-fourths of what remains of the apples. In the morning there is just one apple left. How many apples were there in the bag to begin with?

Step 1 -- Translate

Use variables that make sense.

A = the total number of apples in the bag to begin with

B₁ = number of apples the first brother ate

B₂ = number of apples the second brother ate

We know we started out with an unknown (A) number of apples. Then each brother came along and ate some, leaving just one apple in the bag.

We can now put the above sentence into an equation using our variables.

A = B₁ + B₂ + 1

We also know that the first brother ate three-fourths of the what was first in the bag. That translates to

B₁ = 3/4A

The second brother ate 3/4 of what the first brother left. That translates to

B₂ = 3/4(A - 3/4B₁)

Step 2 -- Substitute

We start with the equation that has the most information

A = B₁ + B₂ + 1

and then substitute what we know into the equation. We know that the first brother ate 3/4A so we can substitute that in for B₁.

A = 3/4A + B₂ + 1

We also know what the second brother ate (see above) so we can substitute that in for B₂

A = 3/4A + 3/4(A - 3/4B₁) + 1

Now that we just need to make one more substitution for B₁ so we have an equation in one variable (A), we can solve for the width. Remembering that the first brother ate 3/4A so we can substitute that in for B₁

A = 3/4A + 3/4(A - 3/4(3/4A)) + 1

Step 3 -- Solve

How many apples were in the bag? We know that

A = 3/4A + 3/4A - 3/4(3/4A) + 1

A = 3/4A + 3/4A - 9/16A + 1

Multiply both sides by 16 to clear the denominators.

16A = 16(3/4A + 3/4A - 9/16A + 1)

16A = 12A + 12A - 9A + 16

16A = 15A + 16

A = 16

So the total number of apples in the bag before the brothers went to bed is 16.

We can verify these answers by substituting them back into the original equation.