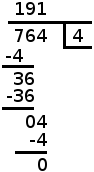ABE Math Tutorials/Whole numbers/Long division

Long division

Introduction

How well do you know your basic division facts? Click here If you would like to review basic division before continuing.

The little sign " ÷ " is not the only one to express a division. No doubt you also remember the division "bar" sign, as in the following example:

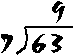
We read this as "seven divided into sixty-three"; and the answer, of course, is still 9. Note ; not over the "6"). that we write the answer (9) over the end of the number it goes into (ie. over the "3" part of 63

Of course, division is easy when the one number goes exactly into another -- we say that 7 divides evenly into 63. But what about numbers which do not divide evenly?

In this case, we divide 7 into 65, instead. Of course, 7 still goes into 65; it still goes in 9 times, so once again we write the 9 over the end of 65. But 7 x 9 is 63 -- so we do that multiplication and we write the "63" under the "65". Then we subtract: 65 - 63 = 2. Our 7 will not go into this 2: the 2 is just "left over". You may remember from your elementary school days that we usually say that there is "2 remainder", and it is customary to show this as a "R2" written up as part of the answer.

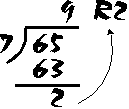
Let's try a longer division problem: 7 divided into 651. (Note: this is exactly the same as saying "651 divided by 7".)

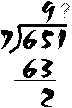
We begin this problem exactly the same as we did the previous one: 7 goes into 65 nine times; 9 x 7 = 63; 65 - 63 = 2. But we are not finished yet! We still haven't done anything with the "1" in "651".. At this point, we "bring down" the one (does this ring a bell?), down beside the "2" which was left over. Now, we divide 7 into "21". Seven goes into 21 three times, so we put the 3 up over the 1. Three times 7 is exactly 21; there are no more digits to be divided, so the problem is finished: 651 ÷ 7 = 93

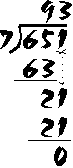
Perhaps you remember this kind of "long division" problem from your elementary school days. Ready to try something more complicated? Try: 6514 ÷ 70. When you're ready, follow the steps below to check your work:

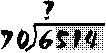
Division with larger numbers takes more steps. How many times does "70" go into "6514"? Let's look at it one digit at a time. First of all, will "70" go into "6"? The answer, of course is no.... Next, let's look at the second digit. Will "70" go into "65"? Not quite...... 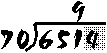Will "70" go into "651"? Yes -- "651" is obviously a lot larger than "70". How many times will it go in? If you try it on a piece of scrap paper, you'll see that 9 x 70 = 630, and 10 x 70 = 700 (too large). So let's write a "9" above the "1" in 651....

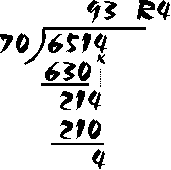and here is the problem completely worked out. We multiplied the "9" times 70 to get 630: now we have 651 - 630 = 21. And now we "bring down" the 4 (the last digit in 6514) and put it beside the "21" to get "214". How many times does 70 go into 214? You'll find that it goes about 3 times. So we put the 3 up above the "4": now, 3 x 70 = 210. We write the "210" right under the "214", and now we subtract: 214 - 210 = 4. There are no more digits left in "6514" to bring down, so our problem is complete. The answer is "93" with 4 remainder ("R4").

Here's a more complicated one to try: 49738 ÷ 351. Did you get 141 (with 247 remainder)? If not, click here for more detail on how this division is solved.

Ready to try a few on your own? (a) 4500 ÷ 50 (b) 2986 ÷ 28 (c) 514736 ÷ 704}}

When you're ready to check your answers for Long Division, click here.

If you're ready for the Long Division homework, click here.